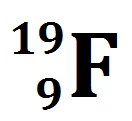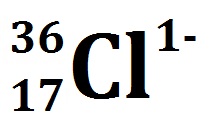Scientific Tutor
Archive for the ‘Chemistry’ Category
Chem – Metals and Non-Metals
How do I tell the difference between metal and non-metal elements?
One important division (organization) of the periodic table that I want to discuss is what is called the metals versus the non-metals. For an example of a periodic table that shows this click here. Keep this periodic table open as you read this and do practice problems. If you look toward the right side of the periodic table you just opened, you will notice that elements toward the upper right hand corner are colored differently (the metals are colored red and the non-metals are colored yellow). These elements are the non-metals. Everything else left of them are metals. The metals also include the two rows on the bottom of the periodic table that seem to be separate. Don’t forget that hydrogen falls into the non-metals. As you can see, most of the elements are metals. In general, metals are not very flexible (they are brittle) and non-metals are very flexible. To compare the two, I like to think of two common items that contain almost pure forms of either a metal or a non-metal. A cooking pot is made up of almost all metal (usually either iron or copper) and they are very difficult to bend and misshape so that is an example of how they are not very flexible. A rubber band is made up of almost all non-metal elements (mostly carbon and hydrogen) and they are very flexible. I am not very concerned that you know the properties of metals versus non-metals because it is not that useful for solving many problems in a standard chemistry class. The information that I mention in the next paragraph is far more important.
The division between the metals and non-metals is most often called the step-stair. They call it that because the line between the metals and non-metals looks like a set of stairs. The main purpose of this section is to be able to identify metals versus non-metals if you have a periodic table in front of you. So if you are givenan element like sulfur, then you would say it is a non-metal. If you are given an element like magnesium, you would say it is a metal. This skill will come in handy, especially in the first half of your chemistry class.
Examples: Using a periodic table, state whether these elements are metals or non-metals.
| Nickle | Metal |
| Uranium | Metal |
| Phosphorus | Non-metal |
PRACTICE PROBLEMS: Using a periodic table. state whether these elements are metals or non-metals.
| Beryllium | Metal |
| Zinc | Metal |
| Iodine | Non-metal |
| Carbon | Non-metal |
| Manganese | Metal |
| Argon | Non-metal |
Chem – Atomic Notation Part 2
What sections should I know before attempting to learn this section?
—> Neutrons
—> Isotopes
—> Periods, Rows, Columns, and Groups
—> Ions
How do I use the periodic table to produce element with atomic notation?
In this section YOU WILL HAVE TO USE THE PERIODIC TABLE as a reference. Now that we have tackled the atomic notation part one section lets us try to reverse the question. What if the question gives you the numbers of protons neutrons and electrons and asks for the atomic notation?
STEP 1) FIRST FOCUS ON THE PROTONS. THE PROTONS WILL TELL YOU WHICH ELEMENT IT IS SO YOU CAN GET THE ELEMENTAL SYMBOL.
STEP 2) NEXT USE THE PROTONS MINUS THE ELECTRONS TO GET THE CHARGE (top right).
STEP 3) THEN USE THE PROTONS PLUS THE NEUTRONS TO THE GET MASS.
VIDEO Atomic Notation Demonstrated Example 4: Given the protons, electrons, and neutrons, create the atomic notation for that element. Use this periodic table as a reference.
The element has 36 protons, 36 electrons, and 40 neutrons.
Fill in the protons (in this case 36) in the bottom left corner.
When we look for the proton number on the periodic table 36 protons means the element Krypton (Kr) so we fill in Kr in the center.
Next we take the protons minus the electrons (36 – 36 = 0) and we get the charge of ZERO. Which means we do not put any notation in the top right corner.
Then we add the protons and neutrons (36 + 40 = 76) to get the atomic mass of 76. We put that in the top left to complete our answer.
Answer:
VIDEO Atomic Notation Demonstrated Example 5: Given the protons, electrons, and neutrons, create the atomic notation for that element. Use this periodic table as a reference.
The element has 15 protons, 18 electrons, and 17 neutrons.
Fill in the protons (in this case 15) in the bottom left corner.
When we look for the proton number on the periodic table 15 protons means the element Phosphorus (P) so we fill in P in the center.
Next we take the protons minus the electrons (15 – 18 = -3) and we get the charge of -3. Which means we put 3- top right corner.
Then we add the protons and neutrons (15 + 17 = 32) to get the atomic mass of 32. We put that in the top left to complete our answer.
Answer:
VIDEO Atomic Notation Demonstrated Example 6: Given the protons, electrons, and neutrons, create the atomic notation for that element. Use this periodic table as a reference.
The element has 20 protons, 18 electrons, and 22 neutrons.
Fill in the protons (in this case 20) in the bottom left corner.
When we look for the proton number on the periodic table 36 protons means the element Calcium (Ca) so we fill in Ca in the center.
Next we take the protons minus the electrons (20 – 18 = 2) and we get the charge of +2. Which means we put 2+ in the top right corner.
Then we add the protons and neutrons (20 + 22 = 42) to get the atomic mass of 42. We put that in the top left to complete our answer.
Answer:
PRACTICE PROBLEMS: Given the protons, electrons, and neutrons, create the atomic notation for that element. Use this periodic table as a reference.
Ion of the element has 7 Protons, 10 electrons, and 7 neutrons.
Answer:
The element has 18 protons, 18 electrons, and 22 neutrons.
Answer:
Ion of the element has 12 protons, 10 electrons, and 13 neutrons.
Answer:
Ion of the element has 24 protons, 21 electrons, and 31 neutrons
Answer:
Chem – Atomic Notation Part 1
What sections should I know before attempting to learn this section?
—> Neutrons
—> Isotopes
—> Ions
What is atomic notation?
DO NOT USE THE PERIODIC TABLE as a reference in this section. When given the atomic notation you should have all the information you need and should not have to look elsewhere. So far we have been looking at the different elements on the periodic table and we have noticed that the atomic number is on top the symbol is in the middle and the mass is on the bottom. This is what they usually call the periodic notation.
However, we have also begun to explore an alternative way to write out that information. This alternative way is called the atomic or nuclear notation. In the atomic notation the atomic mass is on the top left of the elemental symbol, the atomic number (proton number) is on the bottom left, and any charge (if the atom is an ion) is on the top right. Check out the examples below for clarification.
VIDEO Atomic Notation Demonstrated Example 1: If you have the atomic notation of Fluorine below how many protons, electrons, and neutrons would it have?
The 19 at the top left is the atomic mass.So what do we know about the Fluorine atom from this depiction?
The 9 at the bottom left is the proton number.
NO CHARGE at the top right.
So what are some of the questions can we answer about the Chlorine ion from this depiction?
How many protons does it have? 9 protons
How many electrons does it have? 9 – (0) = 9 electrons
How many neutrons does it have? 19 – 9 = 10 neutrons
VIDEO Atomic Notation Demonstrated Example 2: If you have the atomic notation of Chlorine below how many protons, electrons, and neutrons would it have?
So what do we know about the Chlorine ion from this depiction?
The 36 at the top left is the atomic mass.
The 17 at the bottom left is the proton number.
The (1-) at the top right is the charge.
So what are some of the questions can we answer about the Chlorine ion from this depiction?
How many protons does it have? 17 protons
How many electrons does it have? 17 – (-1) = 18 electrons
How many neutrons does it have? 36 – 17 = 19 neutrons
VIDEO Atomic Notation Demonstrated Example 3: If you have the atomic notation of Beryllium below how many protons, electrons, and neutrons would it have?
The 9 at the top left is the atomic mass.So what do we know about the Beryllium ion from this depiction?
The 4 at the bottom left is the proton number (atomic number).
The 2+ at the top right is the charge.
So what are some of the questions can we answer about the Beryllium ion from this depiction?
How many protons does it have? 4 protons
How many electrons does it have? 4 – (+2) = 2 electrons
How many neutrons does it have? 9 – 4 = 5 neutrons
PRACTICE PROBLEMS: Answer the questions below.
How many protons does the element above have? 26 protons
How many electrons does the element above have? 26 – (3) = 23 electrons
How many neutrons does the element above have? 56 – 26 = 30 neutrons
How many protons does the element above have? 19 protons
How many electrons does the element above have? 19 – (1) = 18 electrons
How many neutrons does the element above have? 39 – 19 = 20 neutrons
How many protons does the element above have? 8 protons
How many electrons does the element above have? 8 – (-2) = 10 electrons
How many neutrons does the element above have? 16 – 8 = 8 neutrons
How many protons does the element above have? 35 protons
How many electrons does the element above have? 35 – (-1) = 36 electrons
How many neutrons does the element above have? 82 – 35 = 47 neutrons
How many protons does the element above have? 10 protons
How many electrons does the element above have? 10 – (0) = 10 electrons
How many neutrons does the element above have? 20 – 10 = 10 neutrons
Chem – Ions
What sections should I know before attempting to learn this section?
What are ions?
Ions are charged atoms of an element. You can create a charged atom of an element by a loss or gain electrons. This is because protons are at the center of the atom and therefore cannot be lost or gained. Since electrons are on the outside of atoms they can be lost to gained. So really ions are all about the electrons. Electrons are negatively charged. Therefore, when atoms gain an electron they become a negative ion (anion) or negatively charge and when they lose an electron they become a positive ion (cation) or positively charge.
Adding ONE electron to an atom = -1 charge
Adding TWO electrons to an atom = -2 charge
Taking away ONE electron from an atom = +1 charge
Taking away TWO electrons from an atom = +2 charge
How do we represent ions with elemental symbols?
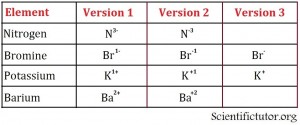
Ions are represented next to elemental symbols by a positive or negative charge and possibly a number on the upper right side of the elemental symbol. Examples of different ways to write the elements are in the pictures below.
How are the ions displayed on the periodic table?
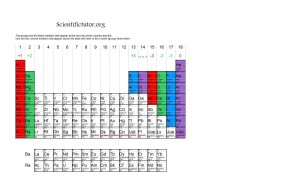
In general, ions are found according to the columns of the periodic table. On most periodic tables, they label the columns 1 through 18 across the top and call them groups. Group 1 starts with Hydrogen and then Lithium. Group 2 starts with Beryllium and then Magnesium. At the end, we have group 18, which starts with Helium and Neon. For now we will only be focusing on group 1,2, 13, 14, 15, 16, and 17. The groups and the ions are best viewed on this periodic table picture below.
Examples: Give the ion of the element and state how many electrons it gained or lost. Use the ion periodic table. VIDEO Ion Examples 1.
| Element | Ion (charged atom) | Electrons |
| Nitrogen | N3- | Gained 3 |
| Bromine | Br1- | Gained 1 |
| Potassium | K1+ | Lost 1 |
| Barium | Ba2+ | Lost 2 |
PRACTICE PROBLEMS: Give the ion of the element and state how many electrons it gained or lost. Make sure you have the ion periodic table link open when answering these questions.
| Element | Ion (charged atom) | Electrons |
| Calcium | Ca2+ | Lost 2 |
| Arsenic | As3- | Gained 3 |
| Fluorine | F1- | Gained 1 |
| Boron | B3+ | Lost 3 |
| Cesium | Cs+ | Lost 1 |
| Sulfur | S2- | Gained 2 |
Chem – Periods, Rows, Columns, and Groups
One immediate division you might have seen on the periodic table is that the elements and their corresponding boxes are organized into vertical (up and down) columns and horizontal (left to right) rows. This link shows a periodic table with the columns (groups) and rows (periods) labeled. You should open that link up and keep it with you to compare with the explanations and examples in this section. In chemistry, we call the vertical organization either columns or groups. Whereas, the horizontal organization is called rows or periods. The columns or groups are usually labeled at the top of the periodic table by numbers; 1 through 18. On they periodic table that you have open one example of a group is group 17. It contains the elements fluorine, chlorine, bromine, iodine, and so on. The periods on most periodic tables are label on the left side of the periodic table by number 1 through 7. On the periodic table you have open one example of is period 4. It contains the elements potassium, calcium, scandium, titanium, and so on. In general, knowing the groups is a lot more important than knowing the periods. A lot of common properties between elements are shared if they are in the same group. For example, fluorine and chlorine are both in the same group and are both gases at a normal room temperature.
Examples: Given the period or group write at least 4 different elements in it.
| Group 15 | N, P, As, Sb, Bi |
| Period 3 | Na, Mg, Al, Si, P, S, Cl, Ar |
PRACTICE PROBLEMS: Given the period or group write at least 4 different elements in it.
| Group 13 | B, Al, Ga, In, Tl |
| Group 2 | Be, Mg, Ca, Sr, Ba, Ra |
| Period 2 | Li, Be, B, C, N, O, F, Ne |
| Group 8 | Fe, Ru, Ir, Mt |
| Period 5 | Rb, Sr, Y, Zr…Ag, Cd, In, Sn, Sb, Te, I, Xe |
Chem – Isotopes
What sections should I know before attempting to learn this section?
—> Neutrons
What are isotopes?
So far we have been talking about the number of neutrons using only the mass numbers on the periodic table. However, those are truly only the average number of neutrons. If we were to look at a random atom, chances are it would have the number of neutrons we have been calculating so far, but that is not always the case. Some atoms of an element don’t have the same atomic mass as they do on the periodic table because they have more or less neutrons than the average number shown on the periodic table. Isotope is a word used to describe how two atoms of the same element can have different numbers of neutrons. Sometimes in a chemistry class, the definition of an isotope is not taught very well so I will also phrase it another way because it could be important to your class. If you have one helium atom with a mass of 4, like it is on the periodic table, and another helium atom with a mass of 5. Those two are isotopes of one another. It is not that the helium with a mass of 4 is the only isotope or that the helium with a mass of 5 is the only isotope. When using the word isotope, you are already suggesting that different atoms of the same element can have different numbers of neutrons. So an isotope will never be used to describe only one atom. It will always be used to describe the differences in neutrons between two or more atoms. Whenever you hear the word isotope you want to immediately think “I am comparing some kind of difference in neutrons”.
Remember your equation for counting neutron from the previous section. neutrons = atomic mass – atomic number.
Examples: Make sure you have this periodic table link open when answering these questions. VIDEO Isotopes Examples 1.
Argon – 42 (Argon that has a atomic mass of 42) is one isotope of argon. How many neutrons does it have?
Answer: 24 neutrons
Antimony – 124 (antimony that has a atomic mass of 124) is one isotope of antimony. How many neutrons does it have?
Answer: 73 neutrons
If you have Nitrogen – 15 and Oxygen – 17 and Sulfur – 34 and Nitrogen – 13 how many of these are isotopes of one another?
Answer: The two nitrogens are isotopes of one another because they have to have the same number of protons but a different number of neutrons.
PRACTICE PROBLEMS: Make sure you have this periodic table link open when answering these questions.
Magnesium – 25 is one isotope of magnesium. How many neutrons does it have?
Answer: 13
Copper – 64 is one isotope of copper. How many neutrons does it have?
Answer: 35
If you have Silicon – 28 and Iodine – 126 and Sulfur – 34 and Iodine – 128 and Silicon – 29 how many of these are isotopes of one another?
Answer: We have two sets of isotopes. One set of isotopes is Silicon – 28 and Silicon – 29. They are isotopes of one another. The second set is Iodine – 126 and Iodine – 128. They are isotopes of one another.
Chem – Neutrons
What sections should I know before attempting to learn this section?
How do I find the neutrons of an element?
Depending on the information you are given there can be many different ways to find the neutrons of an element. We are going to start off by finding the neutrons of an element using the periodic table. Other sections that may help you find he neutrons in a different way (starting with different information) including the sections labeled ISOTOPES or ATOMIC NOTATION.
If you want to find the amount of neutrons an atom of an element has using the periodic table we should first explain where you find that information in each box on the periodic table. The atomic mass is at the bottom of each individual box on the periodic table. It is usually a number with digits that go past the decimal. For the case of Helium, the atomic mass is about 4.002. For most instances of calculation you can just round the atomic mass to the nearest whole number. So 4.002 becomes 4. The word atomic mass can also be know by the words atomic weight, molar mass, or molar weight. All of them mean the same thing as far as you are concerned. Since the vast majority of the atomic mass comes from the protons and neutrons, you can just think of the atomic mass as the protons plus the neutrons. Another way to write that is:
atomic mass = protons + neutrons.
If we know that the protons each contribute 1 mass and the neutrons each contribute 1 mass, then we can come up with a way to determine the amount of neutrons in each element. We simply take the atomic mass minus the atomic number (protons) and we will get the neutrons. Another way to write that is:
neutrons = atomic mass – atomic number.
When you do this remember to round the mass to eliminate the decimal. Like Iron has a mass of 55.85 on the periodic table but you need to round that to 56 when you want to calculate the number of neutrons.
Examples: How many neutrons do each of these elements have according to the periodic table? These are answered with information from this periodic table. VIDEO Determining Neutrons from periodic table Examples 1.
|
Sulfur |
16 |
|
Bromine |
45 |
|
Barium |
81 |
VIDEO Determining Neutrons from the Periodic Table Demonstrated Example 1: How many neutrons does sodium have according to the periodic table? These are answered with information from this periodic table.
What is the symbol for sodium?
Answer: Na
What is the mass for sodium?
Answer: 23 (rounded to the nearest whole number)
What is the atomic number (proton number)?
Answer: 11
What is the formula to solve for neutrons?
Answer:
neutrons = mass – protons
? = 23 – 11
What is the complete answer?
COMPLETE ANSWER: sodium has 12 neutrons according to the periodic table.
PRACTICE PROBLEMS: How many neutrons do each of these elements have according to the periodic table? Make sure you have this periodic table link open when answering these questions.
|
Oxygen |
8 |
|
Chromium |
32 |
|
Potassium |
20 |
|
Mercury |
121 |
|
Chlorine |
18 |
|
Manganese |
31 |
Chem – Protons and Electrons
How do I find the protons and electrons of an element?
Different individual elements can have different amounts of the protons and electrons. Since having different amounts of each of these can determine how different elements can interact with others, scientists have organized them into a sheet called the periodic table. The periodic table is organized first by the number of PROTONS an individual atom of each element has. For the purposes of this section the number of protons will equal the number of electrons.
Each box on the periodic table contains the particular information for an element. At the top of each box is the atomic number. The atomic number is the amount of protons in one atom of that element. If it is a pure element, meaning it has no charge and is not connected to any other elements, then the atomic number also gives you the amount of electrons. In the middle of the periodic notation box is the elemental symbol.
To find different elements on the periodic table it is best to recognize them by the atomic number. As we go across a row (from left to right) the atomic number increases. Once we get to the end of the row on the right, we have to start back at the beginning of the next row on the left. So, the end of the first row is Helium (He). The start of the second row is Lithium (Li). The end of the second row is Neon (Ne) and the beginning of the third row is Sodium (Na). This pattern of increasing atomic number continues all the way through the periodic table. Take a minute to make sure you understand this pattern by trying to look at it on the periodic table.
Examples: How many protons and electrons do these pure elements have according to the periodic table? VIDEO Determining Protons and Electrons from the periodic table Examples 1.
| Neon | 10 protons and 10 electrons |
| Lithium | 3 protons and 3 electrons |
| Silicon | 14 protons and 14 electrons |
PRACTICE PROBLEMS: How many protons and electrons do these pure elements have according to the periodic table?
| Chlorine | 17 protons and 17 electrons |
| Potassium | 19 protons and 19 electrons |
| Boron | 5 protons and 5 electrons |
| Gold | 79 protons and 79 electrons |
| Iodine | 53 protons and 53 electrons |
| Mercury | 80 protons and 80 electrons |
Chem – Periodic Symbols
If we look at the periodic table, we notice that there are different individual boxes. Each of these boxes represents a different element and what a single atom of each element consists of. The different elements are represented by one or more letters. These letters are the elemental symbol. For example, the element hydrogen is represented by H and the element Calcium is represented by Ca. If a letter is uppercase that means it is the first letter in the symbol. If a letter is lowercase that means it is not the first letter in the symbol. For now I want you to focus on getting familiar with the different element names and symbols.
Examples: Give the symbol for the element.
| Helium | He |
| Nitrogen | N |
| Magnesium | Mg |
You should be able think and answer questions in both directions. That is, given the element name tell what the symbol is and given the symbol tell what the element name is.
PRACTICE PROBLEMS: Give the missing symbol or element in the table below. Use this periodic table when solving the problems below.
| H | Hydrogen |
| F | Fluorine |
| Na | Sodium |
| Al | Aluminum |
| Ni | Nickle |
| Be | Beryllium |
| Sn | Tin |
| P | Phosphorus |
| U | Uranium |
| Fe | Iron |
| Ag | Silver |
Unfortunately, you will need to memorize the different symbols for the elements. The sooner you learn them the easier it will be in the future. To help you learn them, I will have you practice throughout the rest of this lesson by forcing you to look them up in order to answer other practice problems. This was the easiest way for me to learn them. I just kept looking at the list of the names and matching them to the symbol. Many times this means you have to scan the periodic table with your eyes and physically look for the symbol. This is very annoying at first, I know, but it is a very useful skill for the future so it is better to suffer through it now rather than later. This link is a list of all the element names and their periodic symbols in alphabetical order in case you can’t find them on the periodic table.
Chem – Matter and the Elements
What is matter and what are the elements?
Matter consists of all the things we interact with physically in our daily lives. Matter is anything that we can physically touch or has a mass. So matter is everywhere. It is in the computer you are reading, the chair you may be sitting in, and even the air around you is made up of matter. The only thing we commonly think of that does not have matter is outer space. Elements are the individual pieces that we can use to build any type of matter we see or touch. You can mix different elements together in different ways to go from something like a computer to a car. The individual pieces are so small we can barely even see them with our most powerful detection equipment.
To know the elements and how to use them better in our every day lives, we have to understand what the individual elements consist of. Elements consist of three different parts. They are the proton, the neutron and the electron. Protons have a large mass and are positively charged. Neutrons have a large mass and do not have a charge. Electrons have a very small mass and have a negative charge.
An individual element by itself is called an atom. If we were to picture an atom of a specific element it would look like a sphere (ball). If we looked inside of the atom we would see the protons and neutrons in the very center of the atom. This very center part of the sphere where the protons and neutrons are is called the nucleus. If we looked for the electrons of this atoms, they would be traveling very fast around the outer edges of the sphere. This is a picture of the atom to match the description I just went through. You don’t need to have a detailed understanding of the structure of an atom yet. As long as you understand that the protons and neutrons are in the middle and the electrons are around the outer parts then you are fine for now.
Even this very simple description and picture of an atom already gives us hints about how the structure of an atom can act. Since the electrons are the outside of the atom we would come into contact with them first. This means that changes that can occur have to change the electrons first. Also, since protons and neutrons are at the center of the atom, they are much harder to change because you have to dig through the outer layers first. Another theory we might come up with is that since protons are positively charged and electrons are negatively charged they might have some kind of attraction toward one another.
Click here for a link to a periodic table. You should have this periodic table or a similar periodic table open throughout the rest of this lesson so you can reference it while you are reading and practicing problems. To emphasize how important the periodic table is for chemistry, I would like to talk about it a little. I tend to complain a lot about how things are organized in science. With the periodic table this is never the case. The more I learn about the elements the more appreciation I have for the periodic table. In my opinion it is the single greatest achievement in science in at least the past 150 years. Anything having to do with modern chemistry owes at least a small portion of its credit to the organization of the periodic table. This is why I would like to thank Dmitri Mendeleev for coming up with the precursor to the modern periodic table. Although, other people we thinking along the same lines at the time and although their may be a better way to organize the periodic table in the future, no one has ever created a periodic table organization that is both so simple to understand and so simple to learn from. Even though it can be complex and confusing when you first look at the periodic table it would be ten or a hundred times worse without it. Throughout most chemistry classes, your ability to get a good grade will depend about 50% on your understanding of the periodic table. No other single factor is nearly as helpful to your grade as knowing as much as you can about the periodic table.
Chem – LESSON 4: The Periodic Table
What is this lesson about?
The periodic table is a tool to organize the elements that we use in chemistry. However, there are many different ways to look at that organization. This lesson explores those different ways to look at the periodic table.
Why is it critical to understand?
Once you are able to look at the periodic table in different ways, then you can also think about how to solve different kinds of problems you may see later in chemistry. Future chemistry lessons, both in your class and on this website, will build off all the information on the periodic table and you will be expected to interpret that information and relate it back to the ways you learned about it in this lesson. How the electrons viewed on the periodic table will be especially important. Since electrons are the outer most regions of an atom they act like the skin of an atom. Our skin determines how we interact with other things outside of ourselves. The “skin” of electrons does the same for the atoms. Whenever other atoms come in contact with each other it is their electrons that interact first and therefore it is their electrons that determine how the two or more atoms will interact when they collide. Depending on how electrons are arranged in an atom will determine things like how bonding works, what ions they can become, and even how they interact with things like light. Many of these concepts will carry over to lessons like electron orbitals and Lewis structures.
New Learning Sections:
—> Neutrons
—> Isotopes
—> Periods, Rows, Columns, and Groups
—> Ions
—> Further Divisions of the Periodic Table
—> Bohr Model and Electron Shells Part 1
—> Bohr Model and Electron Shells Part 2
—> Drawing Valence Electrons Around an Atom
—> College: Causes of Periodic Trends
Reference Pages:
—> Groups and Periods Periodic Table
—> Metal / Non-Metal Periodic Table
—> Elements by Catagories (halogens / alkali metals) Periodic Table
—> Electron Shells Periodic Table
—> Valence Electron Periodic Table
Worksheets:
—> Periodic Table Worksheet 1 WITH ANSWERS
Chem – College: Unit Conversions
What sections should I know before attempting to learn this section?
—> Introduction to Problem Solving
What about more advanced metric unit conversions?
We want to use the units and ratios we discussed in the previous section as mathematical tools for conversions. I will show you how to do one example problem of each of the three ratio techniques. Keep the unit prefixes table open as you are following the problems below.
VIDEO Advanced Unit Conversions Solving Demonstrated Example 1: If you have 1200 ng how many kg is that? (using only the base to decimal ratio)
Step 1:
What numbers and units does the question give you?
Answer: 1200 ng
Step 2:
What units does the question ask for?
Answer: kg
Step 3:
How do we start laying out the problem?
Answer: Put the numbers and units given by the question first.
| 1200 ng | |||
| 1 |
Step 4:
What comes next?
Answer: The units of the answer.
| 1200 ng | kg | ||
| 1 |
Step 5:
What is the first ratio I put between them?
Answer: 0.000 000 001 g / 1 ng, start with units.
| 1200 ng | g | kg | |
| ng |
Step 6:
Fill in the numbers and cross out units
| 1200 ng | 0.000 000 001 g | kg | |
| 1 ng |
Step 7:
What is the second ratio?
Answer: 1000 g / 1 kg, start with units.
| 1200 ng | 0.000 000 001 g | kg | kg |
| 1 ng | g |
Step 8:
Fill in the numbers and cross out units
| 1200 ng | 0.000 000 001 g | 1 kg = | kg |
| 1 ng | 1000 g |
Step 9:
How do I complete the math?
Answer: (1200 * 0.000 000 001) / 1000 = 0.000 000 0012
| 1200 | 0.000 000 001 | 1 kg = | kg |
| 1 | 1000 |
Step 10:
COMPLETE ANSWER: 0.000 000 0012 kg or 1.2 * 10-9 kg
VIDEO Advanced Unit Conversions Solving Demonstrated Example 2: If you have 134 cm how many Mm is that? (using only the power of 10 ratio)
Step 1:
What numbers and units does the question give you?
Answer: 134 cm
Step 2:
What units does the question ask for?
Answer: Mm
Step 3:
How do we start laying out the problem?
Answer: Put the numbers and units given by the question first.
| 134 cm | |||
| 1 |
Step 4:
What comes next?
Answer: The units of the answer.
| 134 cm | Mm | ||
| 1 |
Step 5:
What is the first ratio I put between them?
Answer: 10-2 m / 1 cm, start with units.
| 134 cm | m | Mm | |
| cm |
Step 6:
Fill in the numbers and cross out units.
| 134 cm | 10-2 m | Mm | |
| 1 cm |
Step 7:
What is the second ratio?
Answer: 106 m / 1 Mm, start with units.
| 134 cm | 10-2 m | Mm | Mm |
| 1 cm | m |
Step 8:
Fill in the numbers and cross out units.
| 134 cm | 10-2 m | 1 Mm | Mm |
| 1 cm | 106 m |
Step 9:
How do I complete the math?
Answer: (134 * 10-2) / 106 = 0.000 00134
| 134 | 10-2 | 1 Mm = | Mm |
| 1 | 106 |
Step 10:
COMPLETE ANSWER: 0.000 00134 Mm or 1.34 * 10-6 Mm
VIDEO Advanced Unit Conversions Solving Demonstrated Example 3: If you have 369GL then how many pL is that? (using only the common ratio)
Step 1:
What numbers and units does the question give you?
Answer: 369GL
Step 2:
What units does the question ask for?
Answer: pL
Step 3:
How do we start laying out the problem?
Answer: Put the numbers and units given by the question first.
| 369 GL | |||
| 1 |
Step 4:
What comes next?
Answer: The units of the answer.
| 369 GL | pL | ||
| 1 |
Step 5:
What is the first ratio I put between them?
Answer: 1 000 000 000 L / 1 GL, start with units.
| 369 GL | L | pL | |
| GL |
Step 6:
Fill in the numbers and cross out units.
| 369 GL | 1 000 000 000 L | pL | |
| 1 GL |
Step 7:
What is the second ratio?
Answer: 1 000 000 000 000 pL / 1 L, start with units.
| 369 GL | 1 000 000 000 L | pL | pL |
| 1 GL | L |
Step 8:
Fill in the numbers and cross out units.
| 369 GL | 1 000 000 000 L | 1 000 000 000 000 pL = | pL |
| 1 GL | 1 L |
Step 9:
How do I complete the math?
Answer: (369 * 1 000 000 000 * 1 000 000 000 000) = 3.69 *1023
| 369 | 1 000 000 000 | 1 000 000 000 000 pL= | pL |
| 1 | 1 |
Step 10:
COMPLETE ANSWER: 3.69 * 1023 pL
PRACTICE PROBLEMS: Give the final answer for these questions. Use unit prefixes table if you need.
If you have 15 dag how many cg is that?
Answer: 15000 cg
If you have 27 um how many cm is that?
Answer: 0.0027 cm
How many kilograms are in 49 dg?
Answer: 0.0049 kg
How many megameters are in 98 hm?
Answer: 0.0098 hm
When you finish the lesson, try out the metrics and conversions worksheet.
Chem – Unit Conversions
What sections should I know before attempting to learn this section?
—> Introduction to Problem Solving
How do you convert from one scientific unit to another?
Conversions are taking a number (quantity) with units and changing the number to represent a new set of units. We use these unit conversions in every day life. Whenever you buy more than one item in a store, you are using a unit conversion to calculate the cost. For example, if we say that a person walked 300 meters and a person’s stride is 0.25 meters between the front foot of one step and the front foot of another step, we can now convert between meters and strides. How many strides did that person take? Follow below:
| 300 m | 1 stride = | 1200 strides |
| 0.25 m |
So the answer is 1200 strides. We converted from the unit of meters to the unit of strides.
UNIT CONVERSION CAN BE MADE EASIER BY WHAT I CALL A conversion map. Please open this link and then follow reading the text. A conversion map is simply a guide that you can use to help you through the conversion process. Like a regular map, it has points of interest that you want to go to and streets you have to take to get there. In a conversion map, these “points of interest” are the different units that you want to go from or get to. The “streets” are the conversions or numbers and units that you have to use to get to your “points of interest”. The first conversion map is in the link above and displays the units of kilometers, meters, centimeters, and millimeters. You can see that to go from millimeters to kilometers you have to use two conversions and pass through the units of meters. There are several different versions of conversions maps I have on this website. I have made a different one in each lesson where you learn new units and therefore need to know new conversions. You should use these conversion maps as a guild to help you when you are starting out. Once you get better, help yourself prepare for the test by taking the conversions maps away while you solve practice problems.
VIDEO Unit Conversions Demonstrated Example 1:If you know that a certain length is 3.5 meters. What would that be in centimeters?
Step 1: highlight numbers and units
If you know that a certain length is 3.5 meters. What would that be in centimeters?
Step 2: write numbers and units
3.5m = distance
Step 3: restate the question
? cm = distance
Step 4:
How many conversions must we do?
Answer: Look at the conversion map. We pass through 1 arrow when we go from Meters —> Centimeters. 1 arrows = 1 conversion
Step 5:
How do I start laying out the problem?
Answer: Write out 3 boxes. The first box has the information the question gave us (3.5 m), the second is where we will put the 1 conversion we will have and the last (third) box is where the units that the question asked (cm) for will be.
| 3.5 m | cm | |
| 1 |
Step 6:
What is the first conversion?
Answer: meters (m) to centimeter (cm) ratio
Step 7:
How do I put that in?
Answer: units first, set up the units that need to cancel out (in red)
| 3.5 m | cm = | cm |
| m |
Step 8:
Fill in the numbers next to the units of the conversion (in red)
| 3.5 m | 100 cm = | cm |
| 1 m |
Step 9:
Cross out the units that are found on top and bottom of your conversion.
| 3.5 m | 100 cm = | cm |
| 1 m |
Step 10:
Simplify the problem by getting rid of all the crossing out.
| 3.5 | 100 cm = | cm |
| 1 |
Step 11:
How do I know I am done with conversions?
Answer: The only units left are the units that match the answer. In this case cm.
| 3.5 | 100 cm = | cm |
| 1 |
Step 12:
How do I do the calculations?
Answer: (3.5 * 100) / 1 = 350
| 3.5 | 100 cm = | 350 cm |
| 1 |
Step 13:
COMPLETE ANSWER: 350 cm
VIDEO Unit Conversions Demonstrated Example 2:How many centimeters are in 0.27 kilometers?
What numbers and units does the question give you?
Step 1: highlight numbers and units
How many centimeters are in 0.27 kilometers? What numbers and units does the question give you?
Step 2: write numbers and units
0.27km = distance
Step 3: restate the question
? cm = distance
Step 4:
How many conversions must we do?
Answer: Look at the conversion map. We pass through 2 arrows when we go from Kilometers —> Meters —> Centimeters. 2 arrows = 2 conversion
Step 5:
How do I start laying out the problem?
Answer: Write out 4 boxes. The first box has the information the question gave us (0.27 km), the second and third box are the 2 conversions we will have and the last (fourth) box is where the units that the question asked (cm) for will be.
| 0.27 km | cm | ||
| 1 |
Step 6:
What is the first conversion?
Answer: kilometers (km) to meters (m) ratio
Step 7:
How do I put that in?
Answer: units first, set up the units that need to cancel out (in red)
| 0.27 km | m | cm | |
| km |
Step 8:
Fill in the numbers next to the units of the conversion (in red)
| 0.27 km | 100 m | cm | |
| 1 km |
Step 9:
Cross out the units that are found on top and bottom of your conversion.
| 0.27 km | 1000 m | cm | |
| 1 km |
Step 10:
Simplify the problem by getting rid of all the crossing out.
| 0.27 | 100 m | cm | |
| 1 |
Step 11:
What is the next conversion?
Answer: meters to centimeters ratio
Step 12:
How do I set it up?
Answer: Units first, set up the units that you need to cancel out (in red)
| 0.27 | 1000 m | cm = | cm |
| 1 | m |
Step 13:
Fill in the numbers next to the units of the conversion (in red)
| 0.27 km | 1000 m | 100 cm = | cm |
| 1 km | 1 m |
Step 14:
Answer: Cross out the units that are found on top and bottom of your conversion.
| 0.27 | 1000 m | 100 cm = | cm |
| 1 | 1 m |
Step 15:
Simplify the problem by getting rid of all the crossing out.
| 0.27 | 1000 | 100 cm = | cm |
| 1 | 1 |
Step 16:
How do I know when I am done with the conversions?
Answer: The only units left are the units that match the answer. In this case cm
| 0.27 | 1000 | 100 cm = | cm |
| 1 | 1 |
Step 17:
How do I do the calculations?
Answer: (0.27 * 1000 * 100) / (1*1) = 27000
| 0.27 | 1000 | 100 cm = | 27000 cm |
| 1 | 1 |
Step 18:
COMPLETE ANSWER: 27000 cm or 2.7 * 104 cm
VIDEO Unit Conversions Demonstrated Example 3: If you measure 0.86 mm how many kilometers is that?
Step 1: highlight numbers and units
If you measure 0.86 mm how many kilometers is that?
Step 2: write numbers and units
0.86mm = distance
Step 3: restate the question
? km = distance
Step 4:
How many conversions must we do?
Answer: Look at the conversion map. We pass through 2 arrows when we go from Centimeters —> Meters —> Kilometers. 2 arrows = 2 conversion
Step 5:
How do I start laying out the problem?
Answer: Write out 4 boxes. The first box has the information the question gave us (0.86 mm), the second and third box are the 2 conversions we will have and the last (fourth) box is where the units that the question asked (cm) for will be.
| 0.86 mm | km | ||
| 1 |
Step 6:
What is the first conversion?
Answer: millimeters to meters ratio
Step 7:
How do I put that in?
Answer: units first, set up the units that need to cancel out (in red)
| 0.86 mm | m | km | |
| mm |
Step 8:
Fill in the numbers next to the units of the conversion (in red)
| 0.86 mm | 1 m | km | |
| 1000 mm |
Step 9:
Cross out the units that are found on top and bottom of your conversion.
| 0.86 mm | 1 m | km | |
| 1000 mm |
Step 10:
Simplify the problem by getting rid of all the crossing out.
| 0.86 | 1 m | km | |
| 1000 |
Step 11:
What is the next conversion?
Answer: meters to kilometers ratio
Step 12:
How do I set it up?
Answer: Units first, set up the units that you need to cancel out (in red)
| 0.86 | 1 m | km = | km |
| 1000 | m |
Step 13:
Fill in the numbers next to the units of the conversion (in red)
| 0.86 | 1 m | 1 km = | km |
| 1000 | 1000 m |
Step 14:
Cross out the units that are found on top and bottom of your conversion.
| 0.86 | 1 m | 1 km = | km |
| 1000 | 1000 m |
Step 15:
Simplify the problem by getting rid of all the crossing out.
| 0.86 | 1 | 1 km = | km |
| 1000 | 1000 |
Step 16:
How do I know when I am done with the conversions?
Answer: The only units left are the units that match the answer. In this case km
| 0.86 | 1 | 1 km = | km |
| 1000 | 1000 |
Step 17:
How do I do the calculations?
Answer: 0.86 / (1000 * 1000) = 8.6 * 107
| 0.86 | 1 | 1 km = | 8.6 * 107 km |
| 1000 | 1000 |
Step 18:
COMPLETE ANSWER: 8.6 * 107 km
PRACTICE PROBLEMS: Give the final answer for these questions.
How many centimeters in 78 meters?
Answer: 7800 cm
How many millimeters in 6.3 meters?
Answer: 6300 mm
How many meters in 700 kilometers?
Answer: 700000 m
How many kilometers in 96000 millimeters?
Answer: 0.096 km
If you measure 0.42 cm how many millimeters is that?
Answer: 4.2 mm
If you measure 0.35 m how many kilometers is that?
Answer: 0.00035 km
Chem – Density Problem Solving
What sections should I know before attempting to learn this section?
—> Introduction to Problem Solving
How do you solve density word problems?
To help further your problem solving skills, I will introduce you to the concept of density. Density is the mass per unit volume. Another way to state that is the mass divided by the volume. See equation below:
| Density = | mass |
| volume | |
| 1 | |
| D = | m |
| V |
The letter D represents Density, the letter m represents mass, and the letter V represents volume. The density equation has 3 variables. That means in a problem where you have to use density, you will be given 2 variables and asked to solve for the 3rd. Density can have different units like (g/mL) or (g/L) or (kg/L) or (mg/mL) just to name a few. How do we use it to solve some equations? Look to the demonstrated examples below.
VIDEO Density Problem Solving Demonstrated Example 1: What is the density for a mass that is 345g and 789mL?
Step 1: highlight number and units
What is the density for a mass that is 345g and 789mL?
Step 2: write numbers and units
mass = 345g
volume = 789mL
Step 3: restate the question
density = ?
Step 4:
Now what is a formula or concept that relates together mass, volume, and density?
Answer: the density formula (so write down the density formula below)
| D = | m |
| V |
Step 5:
What next?
Answer: fill in the numbers and units from your steps 1 through 3.
| D = | 345g |
| 789mL |
Step 6:
Solve for density (D)
Answer: 245g / 789mL = 0.437g/mL
Step 7:
COMPLETE ANSWER: D = 0.437g/mL
VIDEO Density Problem Solving Demonstrated Example 2: What is the volume of an object that is 154g and has a density of 67g/L?
Step 1: highlight numbers and units
What is the volume of an object that is 154g and has a density of 67g/L?
Step 2: write numbers and units
mass = 154g
density = 67g/L
Step 3: restate question
volume = ?
Step 4:
Now what is a formula or concept that relates together mass, volume, and density?
Answer: the density formula (so write down the density formula below)
| D = | m |
| V |
Step 5:
What next?
Answer: fill in the numbers and units from your steps 1 through 3.
| 67g/L = | 154g |
| V |
Step 6:
How do you solve for volume?
Answer: First multiply both sides by V
| V * 67g/L = | 154g * V |
| V |
Step 7:
Cross out V on the right side
| V * 67g/L = | 154g * V |
| V |
Step 8:
Simplify
| V * 67g/L = | 154g |
| 1 |
Step 9:
Now divide both sides by 67g/L (red)
| V * 67g/L = | 154g |
| 67g/L | 67g/L |
Step 10:
Cross out 67g/L on the left side
| V * 67g/L = | 154g |
| 67g/L | 67g/L |
Step 11:
Simplify
| V = | 154g |
| 67g/L |
Step 12:
Solve for V
Answer: 154 / 67 = 2.30 L
Step 13:
COMPLETE ANSWER: V = 2.30 L
PRACTICE PROBLEMS: Solve for the missing variable in the word problem.
What is the density of an object with a mass of 25g and a volume of 47mL?
Answer: 0.53g/ml
What is density of something that is 36L and 97g?
Answer: 2.69g/L
What is the mass of a cube that has a density of 42g/mL and a volume of 520mL?
Answer: 21840g
An object is 34L and 369g/L. What is the mass of the object?
Answer: 12546g
What is the volume of an object that has a density of 74g/mL and a mass of 58g?
Answer: 0.78ml
If an object is 23kg and 4kg/L. What is the volume?
Answer: 5.75L
Chem – Introduction to Problem Solving
What sections should I know before attempting to learn this section?
How do you solve word problems in chemistry?
Perhaps the most fundamental problem that most students have in chemistry is the lack of problem solving and organizational skills. I can never overstate how crucial these skills are for doing well in chemistry (and in life). One of the few regrets in all my life is that I did not pick up these skills sooner. Here I will try to lay out as best I can how to think your way through problems to come up with a correct answer. Since word problems are the most common in chemistry and because many people have trouble with them, I will focus my problem solving teaching on them. Improving your problem solving skills will be an ongoing process in any chemistry class, but I will show you the first and most important steps in this section. Be sure to always analyze my demonstrated examples for future insight into problems solving techniques.
Step 1: Underline, highlight, or box the numbers and units in a word problem. Because our brains are not very good at organizing many things at once, we need to show it where it needs to focus the effort. (I know this seems trivial but trust me it helps)
Step 2: Rewrite the numbers and units and identify what they are. Identifying what they are can help you later relate them to formulas or key concepts. (I know this seems trivial but trust me it helps)
Step 3: Restate the question in a short and simple way to guide you to the goal of finishing the question. Again, like the second step, this can help you relate information you already have to formulas or key concepts. (I know this seems trivial but trust me it helps)
Now let us demonstrate this method with some examples. Remember you do not need to answer the problem only organize it. Highlight the numbers and units in the word problems below. Rewrite the numbers and units and identify what they are. Restate the question in a short and simple way.
Examples: VIDEO Problem Solving Examples 1.
Problem Solving Demonstrated Example 1: If an object has mass of 26g and a volume of 55mL what would its density be?
Step 1: highlight numbers and units
If an object has mass of 26g and a volume of 55mL what would its density be?
Step 2: Rewrite numbers and units and identify
26g = mass
55mL = volume
Step 3: Restate question in simple way
density = ?
Step 4:
COMPLETE ANSWER:
26g = mass
55mL = volume
density = ?
Problem Solving Demonstrated Example 2: An increase of 37K would cause the volume to go from 4.0L to 4.8L. What was the original temperature?
Step 1: highlight numbers and units
An increase of 37K would cause the volume to go from 4.0L to 4.8L. What was the original temperature?
Step 2: Rewrite numbers and units and identify
37K = temperature
4.0L = volume
4.8L = volume
Step 3: Restate question in simple way
original temperature = ?
Step 4:
COMPLETE ANSWER:
37K = temperature
4.0L = volume
4.8L = volume
original temperature = ?
PRACTICE PROBLEMS: Highlight the numbers and units in the word problems below. Rewrite the numbers and units and identify what they are. Restate the question in a short and simple way.
1. An object that takes up a volume of 2L and has a mass of 70kg would be what density?
Answer: 2L = volume….70kg = mass….Density = ?
2. If you run a distance of 900m at a time of 380s, what is your speed?
Answer: 900m = distance….380s = time….Speed = ?
3. It takes 15s to fill a 0.7L balloon. What is the rate of air from the container?
Answer: 15s = time….0.7L = volume….Rate = ?
4. If a 20g block takes 60s to heat from 0K to 300K. How long will it take to heat a 38g block of the same substance from 0K to 400K?
Answer: 20g = mass….60s = time….0K = temperature….300K = temperature….38g = mass….0K = temperature….400K = temperature….Time = ?
5. By changing from 78K to 142K the volume increased by 182%. What is the final volume if the original volume was 2.3L?
Answer: 78K = temperature….142K = temperature….182% = percent….2.3L = volume….Final volume = ?
6. Even if the question makes no sense. Picking out 7kg from the hyperbole of a transvector can lead you to 3L in case they ask, what is the density?
Answer: 7kg = mass….3L = volume….Density = ?
Chem – Unit Prefixes
What sections should I know before attempting to learn this section?
What are unit prefixes?
In addition to the basic chemistry units, you also have the prefixes that modify the original unit. They are laid out in this table I have created below that I call the unit prefixes table. Keep this table open as you are learning and practicing through the rest of the chapter.
That looks like a lot of units to memorize but what I want you to focus on the 3 most important ones. Those are milli (m), centi (c), and kilo (k). Look at their last column of information the one called “common ratio”.
Milli means 1,000 times smaller. To put it another way, 1000 millimeters = 1 meter.
You can also write that as a proportion or ratio like I do below:
| 1000 mm |
| 1 m |
or
| 1 m |
| 1000 mm |
No matter how you write out the statement, it means that 1000 millimeters and 1 meter are the same length measurement. The great thing about this is that when you use metric measurements for conversions, you can write out equations in any order you want to as long as they are true statements.
Centi means 100 times smaller. To put it another way, 100 centimeters = 1 meter.
You can also write that as a proportion or ratio like I do below:
| 100 cm |
| 1 m |
or
| 1 m |
| 100 cm |
Kilo means 1000 times bigger. To put in another way, 1 kilometer = 1000 meters.
You can also write that as a proportion or ratio like I do below:
| 1000 m |
| 1 km |
or
| 1 km |
| 1000 m |
To make future questions on homework, a quiz, or a test, memorize these three prefixes above and how to write them as proportions or ratios.
Examples: Write down the ratios in a sentence. Use the unit prefixes table if necessary.
How many centimeters in 1 meter?
Answer: There are 100 centimeters in 1 meter.
How many kiloliters are in 1 liter?
Answer: 1 / 1000 = 0.001……There are 0.001 kiloliters in 1 liter.
PRACTICE PROBLEMS: Write down the ratios in a sentence. Use the unit prefixes table if necessary.
How many milliseconds in 1 second?
Answer: There are 1000 milliseconds in 1 second.
How many centigrams in 1 gram?
Answer: There are 100 centigrams in 1 gram.
How many moles in 1 kilomole?
Answer: There are 1000 moles in 1 kilomole.
How many meters in 1 centimeter?
Answer: 1 / 100 = 0.01……There are 0.01 meters in 1 centimeter.
How many kilograms in 1 gram?
Answer: 1 / 1000 = 0.001……There are 0.001 kilograms in 1 gram.
Chem – Introduction to Units
What are scientific units?
First and most importantly, forget the English system of measurement of pounds and ounces and feet. IT IS USELESS BECAUSE IT IS SO CONFUSING. Not even the English widely use it any more. Doesn’t that tell you something about its’ practicality?
If you are going to pursue any kind of science career, you will have to be good with the metric system. In order to get an A or B in a chemistry class, you at least have to have a decent understanding. If you were raised in the United States like I was, this part of your education was probably denied to you.
Thankfully, in most chemistry classes the percent of the metric system that you have to memorize is fairly small. Below is a table of most of the basic units you will have to know for your chemistry class. Most of these are SI units but not all. MEMORIZE THEM!!!
Chemistry Units:
| Category | Name of unit | Abbreviation |
| mass | Grams | g |
| distance | Meters | m |
| volume | Liters | L |
| time | Seconds | s |
| amount | moles | mol |
| temperature | Kelvin | K |
Below are also some problems to test you after you have done your memorization.
Examples: Identify what category each number and its corresponding units are.
|
Numbers with Units |
Category |
|
240s |
time |
|
3mol |
amount |
|
68g |
mass |
PRACTICE PROBLEMS: Identify what category each number and its corresponding units are.
|
Numbers with Units |
Category |
|
300K |
temperature |
|
25L |
volume |
|
12s |
time |
|
9g |
mass |
|
10mol |
amount |
|
76m |
distance |
Also be able to think and answer the unit questions in the opposite direction like the practice problems below.
PRACTICE PROBLEMS: Identify the abbreviation for each unit category.
|
Category |
Unit Abbreviation |
|
time |
s |
|
distance |
m |
|
volume |
L |
|
amount |
mol |
|
mass |
g |
|
temperature |
K |
Chem – LESSON 3: Metrics and Conversions
What is this lesson about?
This lesson is about the units of measurement chemistry uses and how you can use those units to covert between each other. It also includes and introduction to skills in how to solve word problems, which very often contains the units talked about in this lesson. This problem solving work will also continue throughout many of the chapters but it starts here.
Why is it critical to understand?
Perhaps the most critical science requirement is understanding between two or more people. This is why the scientific units were created. They were meant as a universal language to discuss scientific concepts with other people searching the same kinds of questions. That way any person from any language can analyze mathematical work in science and understand what the person is trying to describe as long as they understand the units. The language of metric units is a language that was created and didn’t come from any natural source. Many people have criticized it and some of those criticisms are very true. However, before this metric system came along most systems of scientific measurement and calculations were much, much worse. Therefore, the metric system is a vast improvement. The sections on problem solving and conversions some of the most common ways that you will see the metric system used. It is nice for a student to be able to identify the metric system, but being able to use the metric system is more important.
New Learning Sections:
—> Introduction to Problem Solving
—> College: Metric Unit Conversions
Reference Pages:
—> Table of Prefixes to Metric Units
Worksheets:
—> Problem Solving Worksheet 1
—> Problem Solving Worksheet 1 WITH ANSWERS
—> Metrics and Unit Conversions Worksheet 1
—> Metrics and Unit Conversions Worksheet 1 WITH ANSWERS
Chem – Multiplication and Division of Scientific Notation
What sections should I know before attempting to learn this section?
—> Exponents
How do you multiply or divide scientific notation?
A lot of students run into trouble when they are trying to multiply or divide scientific notation. Dividing usually creates more problems than multiplying, but I will demonstrate both here just to be sure. Most of the students’ confusion in this area comes from a lack of understanding between their calculator and themselves. Different calculators have what you call different logic. That means different calculators read and interpret what you put into them in different ways. One of the most important lessons to learn early in class is to be comfortable and confident with your calculator. The best way to get good at that is keep trying to punch in the numbers you have in different orders until you get the correct answer.
Multiplying scientific notation is pretty straightforward. Whatever order the number appears in the problem you should punch them in the same order in your calculator. If you want to estimate your answer before you put it in the calculator to help guide you in case you make any mistakes, then you should add together exponents on the 10s when you are multiplying.
Dividing scientific notation can be more complicated. When I meet my students for the first time about 95% of them have problems with dividing scientific notation, so it is nothing to be ashamed of and you are not the only one who is having trouble with it. Like I said before, most of the confusion with this part lies in the use of the calculator. The first and most importance piece of advice I can give a student when dividing scientific notation is to separate each step when doing the divisions. This may seem like a very slow way to go about it at first, but it is absolutely critical to your understanding of how this process works. It is also generally a good way to learn math throughout chemistry. Check out the demonstrated examples below.
In addition to having the abilities to solve multiplication and division problems separately, you also want to know how to solve them together. The last demonstrated example shows you how to combine multiplication and division together.
Examples: Multiply the scientific notation below. VIDEO demonstration of the multiplication of the scientific notation below.
| (8.4 * 103) * (2.7 * 104) = | 2.268 * 108 |
| (1.5 * 10-2) * (7.6 * 105) = | 1.14 * 104 |
| (9.3 * 10-6) * (4.5 * 10-3) = | 4.185 * 10-8 |
VIDEO Dividing Scientific Notation Demonstrated Example 1: Solve the division below.
| 3.2 * 103 = | |
| 4.6 * 10-4 |
First step is to force ourselves to think differently about this problem. To do that we separate the decimal numbers from the 10 to the exponent numbers. This is still mathematically correct.
| 3.2 | 103 = | |
| 4.6 | 10-4 |
Then we can divide each separately. Divide 3.2 by 4.6
| 0.6956 | 103 = | |
| 10-4 |
Now clear your calculator. Then divide 103 by 10-4
| 0.6956 | 107 = | |
| 1 |
Then multiply them back together
| 0.6956 | 107 = | 6.956 * 106 |
| 1 |
COMPLETE ANSWER: 6.956 * 106
VIDEO Dividing Scientific Notation Demonstrated Example 2: Solve the division below.
| 7.8 * 10-5 = | |
| 5.4 * 10-2 |
First step is to force ourselves to think differently about this problem. To do that we separate the decimal numbers from the 10 to the exponent numbers. This is still mathematically correct.
| 7.8 | 10-5 = | |
| 5.4 | 10-2 |
Then we can divide each separately. Divide 7.8 by 5.4
| 1.44 | 10-5 = | |
| 10-2 |
Now clear your calculator. Then divide 103 by 10-4
| 1.44 | 10-3 = | |
| 1 |
Then multiply them back together
| 1.44 | 10-3 = | 1.44 * 10-3 |
| 1 |
COMPLETE ANSWER: 1.44 * 10-3
VIDEO Multiplying and Dividing Scientific Notation Demonstrated Example 1: Solve the multiplication and division of scientific notation problems below.
| (6.9 * 103) * (8.3 * 10-2) = | |
| (8.7 * 10-4) * (1.4 * 107) |
Separate all the numbers.
| 6.9 | 103 | 8.3 | 10-2 = | |
| 8.7 | 10-4 | 1.4 | 107 |
Divide each section separately
| 0.793 | 107 | 5.93 | 10-9 = | |
| 1 |
Then multiply them all together.
| 0.793 | 107 | 5.93 | 10-9 = | 4.7 * 10-2 |
| 1 |
COMPLETE ANSWER: 4.7 * 10-2
PRACTICE PROBLEMS: Solve the multiplication and division of scientific notation problems below.
| (9.2 * 102) * (3.1 * 103) = | 2.852 * 106 |
| (5.4 * 10-3) * (2.6 * 107) = | 1.404 * 105 |
| (7.9 * 10-5) * (1.2 * 10-10) = | 9.48 * 10-13 |
| (3.4 * 10-6) * (9.6 * 10-12) = | 3.264 * 10-17 |
| 2.3 * 102 = | 3.24 * 10-3 |
| 7.1 * 104 |
| 9.6 * 10-3 = | 4.0 * 102 |
| 2.4 * 10-5 |
| 8.5 * 105 = | 2.74 * 107 |
| 3.1 * 10-2 |
| 1.8 * 10-7 = | 4.62 * 10-14 |
| 3.9 * 106 |
| (9.5 * 102) * (4.1 * 103) = | 6.36 * 10-4 |
| (3.6 * 104) * (1.7 * 105) |
| (6.7 * 10-4) * (8.3 * 10-2) = | 3.69 * 104 |
| (5.8 * 10-3) * (2.6 * 10-7) |
| (7.3 * 1013) * (2.5 * 1015) = | 3.56 * 1058 |
| (3.2 * 10-18) * (1.6 * 10-12) |
| (4.9 * 1014) * (2.7 * 10-20) = | 6.96 * 10-3 |
| (3.8 * 10-13) * (5 * 109) |
Of course there are several different ways to think about multiplying and dividing scientific notation. However, the way I explained is the easiest for me to demonstrate and seems to be the easiest for students to learn. If your teachers show you a different way you can use that or you can use mine. In the end they are all the same in terms of the math.
Chem – Scientific Notation Part 2
What sections should I know before attempting to learn this section?
—> Exponents
How do we go from a non-scientific notation number to a scientific notation number?
What happens if we go in the reverse direction? Let’s take a non-scientific notation number and turn it into scientific notation.
VIDEO Scientific Notation Demonstrated Example 3: Convert this non-scientific notation number below into scientific notation.
0.00000000873
What is the first non-zero number we encounter as we go from left to right above?
Answer: 8
What are all the significant figures or numbers after and including 8?
Answer: 873
Where would a decimal point go to make those digits into a number between 1 and 10?
Answer: 8.73
How many places do we have to move our decimal from our original number to get 8.73?
Answer: 9
Therefore, what is the exponent on the 10?
Answer: 9
Is the exponent positive or negative?
Answer: Negative (because we started off with a small number)
What does the scientific notation look like?
COMPLETE ANSWER: 8.73 * 10-9
VIDEO Scientific Notation Demonstrated Example 4: Convert this non-scientific notation number below into scientific notation.
425000
What is the first non-zero number we encounter as we go from left to right above?
Answer: 4
What are all the significant figures or numbers after and including 4?
Answer: 425
Where would a decimal point go to make those digits into a number between 1 and 10?
Answer: 4.25
How many places do we have to move our decimal from our original number to get 4.25?
Answer: 5
Therefore, what is the exponent on the 10?
Answer: 5
Is the exponent positive or negative?
Answer: Positive (because we started off with a large number)
What does the scientific notation look like?
COMPLETE ANSWER: 4.25 * 105
PRACTICE PROBLEMS: Convert these numbers into scientific notation.
| 0.000713 | 7.13 * 10-4 |
| 98000 | 9.8 * 104 |
| 31.2 | 3.12 * 101 |
| 0.0000006508 | 6.508 * 10-7 |
Chem – Scientific Notation Part 1
What sections should I know before attempting to learn this section?
—> Exponents
What is scientific notation?
Now, we will work on what is called scientific notation. It is a way of representing very large or very small numbers while making them easier and more efficient to write out. For this part of the lesson, you will have to understand the idea of exponents, which I explained earlier in the section exponents.
Scientific notation uses powers of 10. Another way of saying that is scientific notation uses exponents attached to a 10.
Examples: Give the regular way to write these scientific notations.
| Scientific Notation | Regular Way |
| 1 * 102 = | 100 |
| 5 * 10-3 = | .005 |
| 3.4 * 109 = | 3,400,000,000 |
In the first two examples, there is not a great difference in the amount of time each would require to write and think about. However, the third example is much harder to think about and write out in the regular way, therefore we use scientific notation. Again, just like I explained in the exponents section, the exponent on the 10 is a measure of how many decimal places you move. For the last example, my decimal place started out between the 3 and the 4. I then moved it 9 places to the right and filled in zeros where I had no numbers before. If you want to know how to put scientific notation into a calculator go to this page: VIDEO how I put this into my calculator. Knowing how to use your calculator on these will help you check on the answers you are getting in the future.
The other critical thing to realize about scientific notation is that the first number in scientific notation has to be between 1 and 10. Look at example 2 and 3 above. Example 2 is 5 * 10-3. 5 is between 1 and 10. Example 3 is 3.4 * 109. 3.4 is between 1 and 10.
We can now try some examples together to help us get the hang of this concept. First, we will try to take a scientific notation and produce the number in the usual way you view it.
VIDEO Scientific Notation Demonstrated Example 1: Write out the number below in non-scientific notation form.
2.6 * 10-4
Where do we start?
Answer: Write down 2.6
What do we look at next?
Answer: The exponent on the 10
Is the exponent negative or positive?
Answer: Negative
What does that mean?
Answer: It means we have to move the decimal left
How many places do we have to move the decimal left?
Answer: 4 (because that is the number in the exponent)
What does it look like after I move the decimal 4 spots to the left?
COMPLETE ANSWER: 0.00026
VIDEO Scientific Notation Demonstrated Example 2: Write out the number below in non-scientific notation form.
1.7 * 106
Where do we start?
Answer: Write down 1.7
What do we look at next?
Answer: The exponent on the 10
Is the exponent negative or positive?
Answer: Positive
What does that mean?
Answer: It means we have to move the decimal right.
How many places do we have to move the decimal right?
Answer: 6 (because that is the number in the exponent)
What does it look like after I move the decimal 6 spots to the right?
COMPLETE ANSWER: 1,700,000
PRACTICE PROBLEMS: Write out the number in non-scientific notation form.
| 6.3 * 103 | 6300 |
| 9.5 * 10-4 | 0.00095 |
| 2.48 * 10-8 | 0.0000000248 |
| 1.678923 * 104 | 16789.23 |
W
Chem – Multiplying and Dividing Significant Figures
What sections should I know before attempting to learn this section?
—> Introduction to Significant Figures
—> Significant Figures Part 4 (All Zeros)
How do you multiply and divide significant figures?
Multiplying and dividing significant figures will require you to give an answer that also has the correct number of significant figures. By contrast, multiplying and dividing is much more common than adding and subtracting in chemistry and therefore, this section will be far most useful than the previous one. Some teachers will demand that you give every numbered answer involved with multiplying and dividing with significant figures. However, it will not be a main focus on this website. Multiplying and dividing significant figures comes down to how many significant figures each number you are given has. Make sure you have reviewed the significant figures sections before you attempt this one. Both multiplying and dividing significant figures have the same rule. That rule is, the FINAL ANSWER of a multiplication and division problem should be rounded to the number of significant figures that is the least amount of any figures used in the multiplication or division. Let us demonstrate below.
Examples: Give the answer to the multiplication and division problems with the correct number of significant figures.
35.6 * 42 = ?
| Problem | Calculator Shows | Correct Answer |
| 42 * 35.6 = | 1495.2 | 1500 |
78.12 / 63.951 = ?
| Problem | Calculator Shows | Correct Answer |
| 78.12 = | 1.221560257… | 1.222 |
| 63.951 |
(357.2 * 2.395) / (169 * 84.756) = ?
| Problem | Calculator Shows | Correct Answer |
| 357.2 * 2.395 = | 0.0597255023… | 0.0597 |
| 169 * 84.756 |
VIDEO Multiplying and Dividing Significant Figures Demonstrated Example 1: What would the answer be to the correct number of significant figures for the problem below?
324 * 56.89 = ?
What answer do I get on calculator when I multiply them?
Answer : 18432.36
How many significant figures is 324?
Answer: 3
How many significant figures is 56.89?
Answer: 4
How many significant figures should the answer be?
Answer: 3 (least amount figures used)
How do I round 18432.36 to 3 significant figures?
COMPLETE ANSWER: 18400
VIDEO Multiplying and Dividing Significant Figures Demonstrated Example 2: What would the answer be to the correct number of significant figures for the problem below?
(3.78 * 9.42) / (5.126 * 7.3) = ?
What answer do I get on calculator when I multiply them?
Answer : 0.95157109337837…
How many significant figures is 3.79?
Answer: 3
How many significant figures is 9.42?
Answer: 3
How many significant figures is 5.126?
Answer: 4
How many significant figures is 7.3?
Answer: 2
How many significant figures should the answer be?
Answer: 2 (least amount figures used)
How do I round 0.95157109337837… to 2 significant figures?
COMPLETE ANSWER: 0.95
PRACTICE PROBLEMS: Determine the answer with the correct significant figures for the problems below.
| 800 * 90 = | 70000 |
| 61.48 / 85 = | 0.72 |
| 0.862 * 1.3659 = | 1.18 |
| 0.00528 / 0.0063 = | 0.84 |
| (21.75 * 40) / (14 * 6.3) = | 10 |
| (96.32 * 17.4) / 237.15 = | 7.07 |
Chem – Adding and Subtracting Significant Figures
What sections should I know before attempting to learn this section?
—> Introduction to Significant Figures
How do you add or subtract significant figures?
Whenever you add or subtract significant figures you have to make sure your answer to that mathematical step reflects the figures that it came from. In terms of addition and subtraction, this focuses around what the decimal places is of the numbers you are adding or subtracting. The number with the least amount of accuracy provides us with a limited amount of decimal places. Let us demonstrate below.
Examples: Give the answer to the addition and subtraction problems with the correct number of significant figures.
78.2 + 63.14 = ?
| Calculator Shows | Correct Answer |
| 141.34 | 141.3 |
3.2 – 76.8914 = ?
| Calculator Shows | Correct Answer |
| –73.6914 | –73.7 |
900 + 320 – 2000 + 60 = ?
| Calculator Shows | Correct Answer |
| –720 | –1000 |
VIDEO Adding and Subtracting Significant Figures Demonstrated Example 1: What would the answer be to the correct number of significant figures for the problem below?
8.635 + 12 = ?
What answer do I get on calculator when I add them?
Answer : 20.635
Which figure has the least amount of decimal places?
Answer: 12
To what decimal place does 12 have?
Answer: the ones place
What decimal place should my answer stop at?
Answer: the ones place
How do I round 20.635 to the ones place?
COMPLETE ANSWER: 21
VIDEO Adding and Subtracting Significant Figures Demonstrated Example 2: What would the answer be to the correct number of significant figures for the problem below?
23 + 700 – 48.1 + 89 = ?
What answer do I get on calculator when I add and subtract them?
Answer : 763.9
Which figure has the least amount of decimal places?
Answer: 700
To what decimal place does 700 have?
Answer: the hundreds place
What decimal place should my answer stop at?
Answer: the hundreds place
How do I round 763.9 to the hundreds place?
COMPLETE ANSWER: 800
PRACTICE PROBLEMS: Determine the answer with the correct significant figures for the problems below.
| 800 + 90 = | 900 |
| 61.48 – 85 = | –24 |
| 0.76 + 1.3659 = | 2.13 |
| 0.00528 + 0.0063 = | 0.0116 |
| 6.3 + 40 – 14 + 21.75 = | 50 |
| 96.32 – 17.4 – 237.15 = | –158.2 |
Chem – Significant Figures Part 4
What sections should I know before attempting to learn this section?
—> Introduction to Significant Figures
—> Significant Figures Part 1 (Zeros to the Left)
—> Significant Figures Part 2 (Zeros Between)
—> Significant Figures Part 3 (Zeros to the Right)
How do you treat each zero you come across?
Once you understand how to treat each ZERO you come across and relate it to where it is compared to the NON-ZEROs then it is time to combine all of your knowledge. Remember, make sure you understand the previous sections of significant figures before you attempt this one. To recap all the rules you have been taught.
ZEROS to the LEFT of NON-ZERO numbers are NEVER significant.
ZEROs BETWEEN NON-ZERO numbers are ALWAYS significant.
If your number DOES NOT show a decimal dot then all the ZEROs to the right of NON-ZERO numbers are NOT significant.
If your number DOES show a decimal dot then all the ZEROs to the right of to the right of NON-ZERO numbers ARE significant.
Examples: Determine the number of significant figures. VIDEO demonstration of the significant figures part 4 from the examples below.
| Measured Number | Number of Significant Figures |
| 0.06104 | 4 |
| 9090 | 3 |
| 0.00280350 | 6 |
| 107.00 | 5 |
| 4000 | 1 |
| 0.0036020700 | 8 |
PRACTICE PROBLEMS: Determine the number of significant figures.
| Measured Number | Number of Significant Figures |
| 201280 | 5 |
| 0.0790 | 3 |
| 0.1060 | 4 |
| 0.005069040 | 7 |
| 7000. | 4 |
| 108830 | 5 |
| 0.09506200 | 7 |
Chem – Significant Figures Part 3
How do we treat ZEROs to the right of NON-ZERO numbers in significant figures?
ZEROs to the right of NON-ZERO numbers are most difficult to determine for significant figures because sometimes they are significant and some times they are not significant. Whether they are significant or not significant all depends on whether the number you are presented with has a decimal dot shown.
If your number DOES NOT show a decimal dot then all the ZEROs to the right of NON-ZERO numbers are NOT significant.
Example: 6800 ← Number of significant figures = 2
If your number DOES show a decimal dot then all the ZEROs to the right of to the right of NON-ZERO numbers ARE significant.
Example: 0.02100 ← Number of significant figures = 4
Examples: Determine the number of significant figures. VIDEO demonstration of the significant figures part 3 from the examples below.
| Measured Number | Number of Significant Figures |
| 73400 | 3 |
| 52.00 | 4 |
| 900000 | 1 |
| 0.085110 | 5 |
| 670. | 3 |
| 0.19500000 | 8 |
PRACTICE PROBLEMS: Determine the number of significant figures.
| Measured Number | Number of Significant Figures |
| 44.000 | 5 |
| 8100 | 2 |
| 3600.00 | 6 |
| 7480. | 4 |
| 6553200 | 5 |
| 0.8200 | 4 |
| 9140.0 | 5 |
Chem – Significant Figures Part 2
How do we treat ZEROs between NON-ZERO numbers in significant figures?
Another easy set of ZEROs we have to deal with are ZEROs BETWEEN NON-ZERO numbers. ZEROs BETWEEN NON-ZERO numbers are ALWAYS significant. So when we go to count significant figures we definitely do count ZEROs between NON-ZERO numbers. These are all the numbers you are already used to counting. So they will be no different from when you are counting number places without using significant figures.
Examples: Determine the number of significant figures. VIDEO demonstration of the significant figures part 2 from the examples below.
| Measured Number | Number of Significant Figures |
| 207 | 3 |
| 1409 | 4 |
| 84005 | 5 |
| .6009 | 4 |
PRACTICE PROBLEMS: Determine the number of significant figures.
| Measured Number | Number of Significant Figures |
| 303 | 3 |
| 90061 | 5 |
| 5407 | 4 |
| .8026 | 4 |
| 4070903 | 7 |
Chem – Significant Figures Part 1
How do we treat ZEROs to the LEFT of NON-ZERO numbers in significant figures?
Since we read from right to left in many languages (including English) usually the first set of ZEROs you come upon are ZEROs to the left of NON-ZERO numbers. ZEROS to the LEFT of NON-ZERO numbers are NEVER significant. This means we DO NOT count them.
Examples: Determine the number of significant figures. VIDEO demonstration of the significant figures part 1 from the examples below.
| Measured Number | Number of Significant Figures |
| 0045 | 2 |
| 0.0031 | 2 |
| 000284 | 3 |
| 0.0000079623 | 5 |
PRACTICE PROBLEMS: Determine the number of significant figures.
| Measured Number | Number of Significant Figures |
| 0.7521 | 4 |
| 00039 | 2 |
| 0582 | 3 |
| 0.006488 | 4 |
| 0.0245976 | 6 |
Chem – Introduction to Significant Figures
What are significant figures?
Significant figures (Sig Figs) or, as some people call them, significant numbers, are a part of science that deals with numbers you get from measuring devices like a scale or a ruler. It is a system to tell you how far you can trust your measurement numbers or to put it another way, how accurate they are. What you do for significant figures is count each place (decimal place) in any figure or number you are given.
For example:
96000
How many number places are in 96000? 5
How significant figures are in 96000? 2
What I am trying to highlight is that there is a difference between how many number places (decimal places) that are shown in a written number and how many we actually count in science (significant figures). Throughout the rest of this section I will teach you how to count the significant figures correctly, but first let us talk about the terminology around significant figures.
What is the terminology surrounding significant figures?
When we describe how to break down significant figures we divide numbers (0 to 9) into two categories. The first category is the ZERO. Zeros can mean different things in science so we have to make a special category for them. The second category is the NON-ZERO numbers (1,2,3,4,5,6,7,8,9). All the non-zero numbers are treated the same way when we use significant figures so they all go in the same category.
We can further break down ZEROS into where they are relative to the NON-ZERO numbers. ZEROs can be three different places.
ZEROs can be to the LEFT of NON-ZERO numbers. Example: 0.0047
ZEROs can be BETWEEN NON-ZERO numbers. Example: 2008
ZEROs can be to the RIGHT of NON-ZERO numbers. Example: 6300
Examples: Determine if the number has ZEROs BETWEEN, to the RIGHT of, or to the LEFT of NON-ZERO numbers. More than one answer is possible. VIDEO demonstration of determining where the ZEROs are from the examples below.
| Number | Where are ZEROs? |
| 0.00145 | Left |
| 2500 | Right |
| 84005 | Between |
| 0.07009 | Left and Between |
| 03108600 | Left and Between and Right |
PRACTICE PROBLEMS: Determine if the number has ZEROs BETWEEN, to the RIGHT of, or to the LEFT of NON-ZERO numbers. More than one answer is possible.
| Number | Where are ZEROs? |
| 420 | Right |
| 0.837 | Left |
| 0.05206 | Left and Between |
| 3014 | Between |
| 0.6705090 | Left and Between and Right |
Chem – LESSON 2: Significant Figures and Scientific Notation
What is the lesson about?
This lesson is about how the numbers of chemistry are read and written. The reason that they are different from other non-scientific or non-mathematical number is because many numbers in science are either very small or very large. They also help us to make quick estimations if needed.
Why is critical to understand?
From here on out many of the numbers in chemistry will be written in the format that you see in this lesson. If you are not able to learn that format, then you will not be able to understand possible numbers in other lessons. This lesson also makes it easier to compare very large and small numbers that can help you visualize concepts in your head.
New Learning Sections:
—> Introduction to Significant Figures
—> Significant Figures Part 1 (Zeros to the Left)
—> Significant Figures Part 2 (Zeros Between)
—> Significant Figures Part 3 (Zeros to the Right)
—> Significant Figures Part 4 (All Zeros)
—> Adding and Subtracting Significant Figures
—> Multiplying and Dividing Significant Figures
—> Multiplying and Dividing Scientific Notation
Reference Pages:
NONE
Worksheets:
—> Significant Figures and Scientific Notation Worksheet 1
—> Significant Figures and Scientific Notation Worksheet 1 WITH ANSWERS
Chem – Solving for an Unkown
What sections should I know before attempting to learn this section?
–-> Equations
How do you solve for an unknown?
Besides multiplication and division, the most important mathematical skill you will need for this class is the ability to perform algebra manipulations to solve for an unknown variable like “x”. It is essential that you learn this skill early on in chemistry and continue to excel at it throughout the class. It is also useful in physics, if you plan to take that class in the future. If you get frustrated, keep in mind that I learned all I needed to know about math and solving for unknowns in a chemistry class and not in a math class. Anyone can learn this skill if they practice.
The central rule for algebra and solving for an unknown is that you always have to preform the same math function on both sides of an equal sign.
FIRST EXAMPLE if you have the equation:
|
45 = |
7 |
|
z |
You can multiply both sides by z (* z) like below
|
z * 45 = |
7 * z |
|
z |
SECOND EXAMPLE is if you had the equation:
|
3x = |
4 |
|
1 |
1 |
You can divide both sides by 3 like below
|
3x = |
4 |
|
3 |
3 |
Now that we know what is possible with equations, let us get to the core of how we should think about solving for unknowns. In my years of teaching, I have found a simple way to go about solving for unknowns that seems to make sense to almost every student I meet. It is a process that follows 2 goals.
Goal One: Get the unknown (the letter) into the numerator using multiplication or cross multiplication.
Goal Two: Get the unknown (the letter) alone on one side of the equation usually through the use of division.
That is it. Those are your only goals with 99% of the math problems you run across in chemistry. Now that we know what our goals are, let us take a look at some examples of using those goals. REMEMBER ONLY SOLVE ONE STEP AT A TIME AND WRITE OUT EACH AND EVERY STEP.
VIDEO Solving for an Unknown Demonstrated Example 1:
Given the equation, solve for the unknown X
|
5X = |
8 |
|
1 |
1 |
Step 1:
What is your first goal? Get the unknown into the numerator.
Has this been done? Yes, so we do not need to worry about it.
Step 2:
What is our second goal? Get the unknown alone on one side.
Has this been done? No.
So what do we need to do to achieve this? Divide both sides by 5 to move it away form the X.
|
5X = |
8 |
|
5 |
5 |
Step 3:
Cross out the 5 on the left side.
|
5X = |
8 |
|
5 |
5 |
Step 4:
Simplify
|
X = |
8 |
|
5 |
Is the unknown alone on one side? Yes. Okay then solve.
Step 5:
Solve: 8 / 5 = 1.6
COMPLETE ANSWER: X = 1.6
VIDEO Solving for an Unknown Demonstrated Example 2:
Given the equation, solve for the unknown V
|
56 = |
8V |
|
9 |
Step 1:
What is your first goal? Get the unknown into the numerator.
Has this been done? Yes, so we do not need to worry about it.
Step 2:
What is our second goal? Get the unknown alone on one side.
Has this been done? No.
So what do we need to do to achieve this? Divide both sides by 8 to move it away form the V.
|
56 = |
8V |
|
9 * 8 |
8 |
Step 3:
Crossing out the 8 on the right side.
|
56 = |
8V |
|
9 * 8 |
8 |
Step 4:
Simplify
|
56 = |
V |
|
9 * 8 |
Is the unknown alone on one side? Yes. Okay then solve.
Step 5:
Solve: 56 / (9 * 8) =
COMPLETE ANSWER: V = 0.78
VIDEO Solving for an Unknown Demonstrated Example 3:
Given the equation, solve for the unknown P
|
4 = |
7 |
|
P |
2 |
Step 1:
What is your first goal? Get the unknown into the numerator.
Has this been done? No.
So what do we need to do to achieve this? Cross multiply the P and the 2.
|
2 * 4 = |
7 * P |
|
P |
2 |
Step 2:
Cross out the P on the bottom left and the 2 on the bottom right.
|
2 * 4 = |
7 * P |
|
P |
2 |
Step 3:
Simplify
|
2 * 4 = |
7 * P |
|
1 |
Is the unknown in the numerator? Yes. Okay time to focus on our second goal.
Step 4:
What is our second goal? Get the unknown alone on one side.
Has this been done? No.
So what do we need to do to achieve this? Divide both sides by 7 to move it away form the P.
|
2 * 4 = |
7 * P |
|
7 |
7 |
Step 5:
Crossing out the 7 on the right side.
|
2 * 4 = |
7 * P |
|
7 |
7 |
Step 6:
Simplify
|
2 * 4 = |
P |
|
7 |
Is the unknown alone on one side? Yes. Okay then solve.
Step 7:
Solve: (2 * 4) / 7 = 0.86
COMPLETE ANSWER: P = 0.86
VIDEO Solving for an Unknown Demonstrated Example 4:
Given the equation, solve for the unknown R
|
78 = |
3 * 5 |
|
R |
Step 1:
What is your first goal? Get the unknown into the numerator.
Has this been done? No.
So what do we need to do to achieve this? Multiply the R and to both sides.
|
R * 78 = |
3 * 5 * R |
|
R |
Step 2:
Cross out the R on the Right.
|
R * 78 = |
3 * 5 * R |
|
R |
Step 3:
Simplify
|
R * 78 = |
3 * 5 |
|
1 |
Is the unknown in the numerator? Yes. Okay time to focus on our second goal.
Step 4:
What is our second goal? Get the unknown alone on one side.
Has this been done? No.
So what do we need to do to achieve this? Divide both sides by 78 to move it away form the P.
|
R * 78 = |
3 * 5 |
|
78 |
78 |
Step 5:
Crossing out the 78 on the left side.
|
R * 78 = |
3 * 5 |
|
78 |
78 |
Step 6:
Simplify
|
R = |
3 * 5 |
|
78 |
Is the unknown alone on one side? Yes. Okay then solve.
Step 7:
Solve: (3 * 5) / 78 = 0.19
COMPLETE ANSWER: R = 0.19
PRACTICE PROBLEMS: Given the equation, solve for the unknown.
Given the equation solve for G
|
4G = |
9 |
| 1 |
Answer: 2.25
Given the equation solve for T
|
13 * 2 = |
5T |
| 1 |
Answer: 5.2
Given the equation solve for H
|
8 = |
5 |
|
H |
6 |
Answer: 9.6
Given the equation solve for K
|
2 * 9 = |
47 |
|
3 |
K |
Answer: 7.83
Given the equation solve for E
|
4 = |
16 |
|
E |
Answer: 0.25
Given the equation solve for
|
50 = |
8 * 6 |
|
B |
Answer: 0.96
When you finish the lesson, try out the math review worksheet.
Chem – Equations
What are equations?
Simply put, equations are anything that have an equal sign in them.
Examples:
|
3x = |
4 |
|
5 = |
8y |
|
2 |
|
41 = |
7 |
|
z |
What we need to focus on the most is a different way to view equations that will become useful in the next section solving for an unknown and will remain useful whenever we use math in chemistry or in any course in the future.
You want to look any equation and break it down into 4 different quadrants. Part of the reason I display math the way I do on this website is to help promote this thinking. If we look below, I have separated the equation into 4 different boxes. Remember if a quadrant is empty you can always fill in a ONE and not change the equation.
VIDEO Equations Demonstrated Example 1:
Say what expression is in each quadrant
|
6y = |
13 |
|
9 |
8 |
Step 1:
In the TOP LEFT quadrant is the 6y
|
6y = |
13 |
|
9 |
8 |
Step 2:
In the TOP RIGHT quadrant is the 13
|
6y = |
13 |
|
9 |
8 |
Step 3:
In the BOTTOM LEFT quadrant is the 9
|
6y = |
13 |
|
9 |
8 |
Step 4:
In the BOTTOM RIGHT quadrant is the 8
|
6y = |
13 |
|
9 |
8 |
VIDEO Equations Demonstrated Example 2:
Say what expression is in each quadrant
|
7 = |
1 |
|
24 |
4 * P |
Step 1:
In the TOP LEFT quadrant is the 7
|
7 = |
1 |
|
24 |
4 * P |
Step 2:
In the TOP RIGHT quadrant is the 1
|
7 = |
1 |
|
24 |
4 * P |
Step 3:
In the BOTTOM LEFT quadrant is the 24
|
7 = |
1 |
|
24 |
4 * P |
Step 4:
In the BOTTOM RIGHT quadrant is the 4 * P (which is the same as 4P)
|
7 = |
1 |
|
24 |
4 * P |
VIDEO Equations Demonstrated Example 3:
Say what expression is in each quadrant
|
30 = |
5 |
|
H |
Step 1:
In the TOP LEFT quadrant is the 30
|
30 = |
5 |
|
H |
Step 2:
In the TOP RIGHT quadrant is the 5
|
30 = |
5 |
|
H |
Step 3:
In the BOTTOM LEFT quadrant is the 1 (because it was empty I can put a 1 there)
|
30 = |
5 |
|
1 |
H |
Step 4:
In the BOTTOM RIGHT quadrant is the H
|
30 = |
5 |
|
H |
PRACTICE PROBLEMS: Give the numbers or letters in the quadrant that they ask about.
What is in the TOP LEFT quadrant?
|
52 = |
6s |
|
3 |
4 |
Answer: 52
What is in the BOTTOM LEFT quadrant?
|
1 = |
5 |
|
2y |
H |
Answer: 2y
What is in the TOP RIGHT quadrant?
|
42 = |
75 |
|
6f |
8 |
Answer: 75
What is in the BOTTOM RIGHT quadrant?
|
5 = |
61 |
|
13z |
Answer: 1
What is in the BOTTOM LEFT quadrant?
|
4 = |
9u |
|
35 |
Answer: 1
Chem – Greatest Common Divisor
Next, we tackle the concept of the greatest common divisor. This is something you most likely used in math when you were working on chapters with fractions in them. The greatest common divisor is commonly used in math when you are creating fractions in the lowest terms possible. Simply put, the greatest common divisor is a number (for our purposes, only integers) that is the largest possible number you can divide into a group of two or more numbers. This concept will be used in a very limited way throughout the first half of the chemistry class.
Examples: Give the greatest common divisor between these two numbers. VIDEO demonstration of the greatest common divisor examples below.
| 8 and 10 | 2 |
| 100 and 25 | 25 |
| 36 and 45 | 9 |
So for the first example, I tried going up from the bottom of the integer scale. I started with 1. 1 divides into 8 and 10. Let’s try going up then. 2 divides into 8 and 10. 3 does not. 4 does not. This is the point where I will usually stop. So, the only answer I am left with is 2.
PRACTICE PROBLEMS: Find the greatest common divisor.
| 25 and 10 | 5 |
| 14 and 28 | 7 |
| 12 and 9 | 3 |
| 33 and 55 and 121 | 11 |
Chem – Least Common Multiple
The least common multiple is something you will need to know for a couple of the coming lessons in the first half of chemistry. What is the least common multiple? Well if you take two or more numbers like 2 and 3 and try to find a new and higher number that is a common multiple to both of them that is your greatest common multiple. In this case the least common multiple for 2 and 3 would be 6. If you multiply 2 by 3 it = 6. If you multiply 3 by 2 it = 6. As you can see a quick way to find a common multiple is to multiply together the two numbers you are trying to deal with. This will always give you a common multiple. However, it will not always give you the LEAST COMMON MULTIPLE.
Examples: Give the least common multiple between these numbers. VIDEO demonstration of the least common multiple examples below.
| 4 and 5 | 20 |
| 8 and 7 | 56 |
| 4 and 2 | 4 |
| 6 and 12 | 12 |
PRACTICE PROBLEMS: Give the least common multiple between these numbers.
| 3 and 4 | 12 |
| 6 and 5 | 30 |
| 1 and 6 | 6 |
| 48 and 6 | 48 |
Chem – Exponents
One representation or function that a lot of people can be unfamiliar with is the exponent. Simply put, exponents are causing a chain of multiplication events. For example, 10 with an exponent of 6 (looks like this: 106 or 10^6) means that you take 10 and multiply it by 10, 6 times in a row. The formula is: 10*10*10*10*10*10. Exponents can also appear with a negative in front of them, like 10-4. The formula for this one is: 10 / 10 / 10 / 10. So they are the opposite of each other. If you have a positive exponent, you multiply, and if you have a negative exponent, you divide. If you are unsure how to input exponents into a calculator, then go to this page: VIDEO How do I put exponents into my calculator? The link in previous sentence includes demonstrations of the examples below.
Numerical exponents should only be shown as a number in the upper position next to other numbers. Exponents will not be shown next to letters of elements (this is a charge which we will discuss in a later lesson). So for an example of what I mean, you can write 54 and that is an exponent. However, if I write out S-2, that is not an exponent.
Examples: Provide the answers for these exponent problems. VIDEO How do I put exponents into my calculator?
| 22 = 2*2 | 4 |
| 56 = 5*5*5*5*5*5 | 15625 |
| 6-3 = 1 / (6*6*6) | 1/216 |
Exponents will be used throughout chemistry, but they are usually very common when it comes to a concept called scientific notation, which will be discussed in the next lesson. In scientific notation, the focus is on exponents of 10, as illustrated in the examples below.
Examples: Provide the answers for these exponent problems. VIDEO How do I put exponents into my calculator?
| 103 = 10*10*10 | 1,000 |
| 10-4 = 1 / (10*10*10*10) | .0001 |
| 105 = 10*10*10*10*10 | 100,000 |
You can input these problems into your calculator and work them out that way, but as you get further into chemistry, you might want to use a trick to make finding exponents of 10 faster and easier for you. This trick involves moving the decimal to the right or left, depending on if it is a positive or negative exponent. If it is a positive exponent of 10, then you move the decimal to the right however many spaces the exponent number is. In the previous example of 103, You start off with 1.0 : if you move the decimal to the right once, you get 10 : if you move the decimal to the right again, you get 100 : and if you move the decimal to the right yet again, you get 1000. How many times did we move the decimal? Answer: 3. That is because the exponent was 3.
PRACTICE PROBLEMS: Give the regular (non-exponent number) for the exponent problems below problems.
| 10-2 | .01 |
| 106 | 1,000,000 |
| 109 | 1,000,000,000 |
| 10-7 | .0000001 |
Chem – Proportions and Ratios
Proportions or ratios are an important part of math in chemistry. They are normally used when comparing two different elements, compounds, or amounts. Don’t let the two words confuse you. They are actually the same thing. A proportion is a ratio and and ratio is a proportion. I know some math fanatics out there may argue that last statement with me but this a science website so I don’t care. Most importantly, what is a proportion or ratio? Quite simply, a proportion or ratio is just a type of division.
For example, the ratio of apples to oranges can be written in either of the two ways below:
| Apples |
| Oranges |
Or
Apples/Oranges
Notice in both cases the thing (apples) that was asked about first in the ratio goes on top (the numerator) and the thing (oranges) that was asked about second goes on bottom (the denominator). It will be like this for all proportions or ratios unless specifically stated otherwise.
Let us demonstrate another example. If I have 40 apples total in baskets, and each basket carries 10 apples, what is the proportion of a single basket of apples to the total apples?
| 10 apples = | 1 = | 0.25 |
| 40 apples | 4 |
For most proportion or ratio questions, the preferred representation of the answer from my example should be ¼ or 1 to 4 or 1 per 4. However, if I punch the solution into a calculator, I would get 0.25, which is the same answer but sometimes can be difficult to interpret. Again, you state the numerator first and then the denominator second. Now that you are familiar with these examples, try some practice problems on your own.
PRACTICE PROBLEMS: Solve the proportions or ratios below.
If there are 7 boys and 21 girls in a class, what is the ratio of girls to boys?
Answer: 3/1 or…..3 to 1 or……3 girls to 1 boy
From the information in the question above, what is the ratio of boys to total number of people in the class?
Answer: ¼ or……1 to 4 or…….1 boy to 4 people
If you have 80 squirrels for every 5 acres, what is the ratio of squirrels to acres?
Answer: 16/1 or……16 to 1 or……..16 squirrels for every acre
If you have 108 ounces of soda and 9 cans, what is the proportion of soda to cans?
Answer: 12/1 or……12 to 1 or………12 ounces per can
s per can
Chem – Percentages
Percentages are very useful in chemistry. A percent is used in chemistry usually when we are trying to dissect something that has multiple parts. We describe each part as being a percent of the total. The percentage should always be the same even when we are dealing with a small or large amount of the same thing. Let’s go through an example.
Examples:
If a 100-box crate of ice cream is delivered to the ice cream store on a slow business day and 20% of the ice cream is vanilla, how many boxes are vanilla?
20% of 100 =
or
0.20 * 100 =
Answer: 20.
However, if a 200-box crate of ice cream is delivered to the ice cream store on a busy business day and 20% of the ice cream is vanilla, how many boxes are vanilla?
20% of 200 =
or
0.20 * 200 =
Answer: 40
We can learn from this example that the amount of something (the number of boxes) does not affect the percentage. The percentage does not care if we have 100 boxes or 200 boxes or a million boxes. This gives us an advantage in some chemistry problems because that means we can use whatever amount we want because it will not affect the percentage.
The other thing worth noting in the examples is that you can convert a percentage to a decimal. In the first example, 20% and 0.20 are the same thing. This can be very helpful if you want to multiply or divide a percentage.
If you want to take a percent and turn it into a decimal, then you move your decimal point two spaces to the left. If you want to take a decimal and turn it into a percent, then you take your decimal point and move it two spaces to the right.
Examples: Give the decimal of the percent. VIDEO demonstration of the percentages and decimals below.
| 45% | 0.45 |
| 130% | 1.3 |
| 5% | 0.05 |
| 783% | 7.83 |
PRACTICE PROBLEMS: Fill in the equivalent decimal or percentage.
| 78% | 0.78 |
| 36% | 0.36 |
| 2% | 0.02 |
| 96% | 0.96 |
| 265% | 2.65 |
| 9% | 0.09 |
Chem – Multiplication and Division Together
How do you do Multiplication and Division on a calculator?
The way that division problems can be written like fractions is usually the most useful in science. It is the most common way written and the easiest to think about when you have to do any rearrangements of equations. In future chapters, we will also try working with multiplication and division simultaneously, and we have to know how to deal with that.
Examples: Solve the combined multiplication and division problems. I demonstrate how these examples are put into your calculator with these two different links. VIDEO Multiplication and division examples with a regular calculator. VIDEO Multiplication and division with a graphing calculator.
| 50 / ((2)(5)) = | 5 |
| (6*10) / (2 *4(5)) = | 1.5 |
| (15 * 2) / 3 = | 10 |
Another way to represent multiplication and division problems is to weave them together into what teachers will call “train tracks” or multiplying by ratios. Due to restrictions on how I am able to write math examples out on a word processor, I will explain my example after I write it.
Examples: Solve the combined multiplication and division problems. They are demonstrated by the links in the examples above.
| 10 | 15 | 5 = | 12.5 |
| 30 | 2 |
The above means: (10 * 15 * 5) / (30 * 2) = 12.5
| 20 | 1 | 8 = | 8 |
| 4 | 2.5 | 2 |
The above means: (20 * 1 * 8 ) / (4 * 2.5 * 2) = 8
PRACTICE PROBLEMS: Solve the following problems.
| 8 | 6 | 10 |
| 2 | 4 | 3 |
The above = 20
| 3.8 | 2.1 | 7.6 |
| 2.5 | 9.6 | 1.1 |
The above = 2.30
| 12 | 82 | 36 |
| 70 | 2 | 54 |
The above = 4.69
| 5.6 | 3.1 | 2.3 |
| 1.8 | 10.4 | 9.2 |
The above = 0.23
Chem – Division
How do you do Division on a calculator?
With multiplication, the order in which you multiply does not matter, but with division, it can often be critical. So if you get stuck in the examples and practice problems, try punching them your calculator buttons in a different order to see if that makes any difference.
Examples: These are the ways division can be written. I demonstrate how these examples are put into your calculator with these two different links. VIDEO Division examples with a regular calculator. VIDEO Division with a graphing calculator.
| 16 divided by 4 = | 4 |
| 3 divided into 9 = | 3 |
| 10 / 5 = | 2 |
In text I will tend to write division like below
| 45 = | 9 |
| 5 |
| 63 = | 21 |
| 3 |
| 28 = | 0.28 |
| 100 |
PRACTICE PROBLEMS: Solve these division problems.
| 5 divided into 20 = | 4 |
| 6 divided by 12 = | 0.5 |
| 30 / 6 = | 5 |
| 40 divided into 10 = | 0.25 |
| 3/9 = | 0.33 |
| 60 / 15 = | 4 |
| 12 = | 4 |
| 3 |
| 74 = | 37 |
| 2 |
| 16 = | 0.32 |
| 50 |
Chem – Multiplication
How do you do multiplication on a calculator?
The first thing we need to understand for chemistry is how different math signs can be written. I will skip addition and subtraction because those are very straight forward and not as commonly used throughout the material you will need for the chemistry class. That leaves multiplication and division. In this section I will tackle how multiplication can appear in different ways and how to use your calculator to solve multiplication problems. In the next section on division I will answer questions about division.
Some people can get confused if I use the (x) symbol for multiplication because they have been taught in math that “x” can represent a variable. Therefore, on most of this website I will try not to use the “x” for multiplication. Instead I prefer to use the (*) symbol or parentheses to represent multiplication.
Examples: These are the ways multiplication can be written. I demonstrate how these examples are put into your calculator with these two different links. VIDEO Multiplication examples with a regular calculator. VIDEO Multiplication with a graphing calculator.
| 5 times 3 = | 15 |
| 6 x 2 = | 12 |
| 4 * 5 = | 20 |
| 7(3) = | 21 |
| (8)(9) = | 72 |
In text I tend to write multiplication like below
| 5 | 7 = | 35 |
| 3 | 9 = | 27 |
| 20 * 4 | 8 * 6 = | 3840 |
PRACTICE PROBLEMS: Tell me what the answers are to these problems.
| 12 times 3 = | 36 |
| 50 x 4 = | 200 |
| 33 * 2 = | 66 |
| 6(0) = | 0 |
| (10)8 = | 80 |
| 4(5)2(3) = | 120 |
| 3 | 2 = | 6 |
| 4 | 6 = | 24 |
| 12 * 5 | 9 * 7 = | 3780 |
Chem – LESSON 1: Math Review
If your math is very strong you can skip this lesson.
I start off with the mathematical side of chemistry for a very specific reason. Many people struggle with this part, as I did when I first started. However, if you cannot get past this first lesson or first test without a B or A on the test you will most likely not be able to pass the second half of chemistry. For a college student (or AP student), it is critical to know early on if they are going to be able to handle a class or if they have the drop it in the first two weeks. I want to emphasize that any college (or AP) students who struggle with this MATH REVIEW LESSON should seriously think about dropping the class. After you have dropped the class, try learning the material you received in the first two weeks, or the material on my website, before thinking about starting the same chemistry class again. High school students would be wise to work hard on this chapter, but they do have far more time to review the material when it becomes critical later on.
It is sad to say that I myself learned more math in science than I ever did in math. Therefore, it is possible even if you are not the best at math, to learn all you need to know right now and throughout the chemistry class. Below are the different sections of the math review lesson.
New Learning Sections:
—> Division
—> Multiplication and Division Together
—> Percentages
—> Exponents
—> Equations
Reference Pages:
None
Worksheets:
—> Math Review Worksheet 1 WITH ANSWERS
Chem Misc – Elements Alphabetical Order
| Element Name | Symbol | Atomic Number |
| Actinium | Ac | 89 |
| Aluminum | Al | 13 |
| Americium | Am | 95 |
| Antimony | Sb | 51 |
| Argon | Ar | 18 |
| Arsenic | As | 33 |
| Astatine | At | 85 |
| Barium | Ba | 56 |
| Berkelium | Bk | 97 |
| Beryllium | Be | 4 |
| Bismuth | Bi | 83 |
| Bohrium | Bh | 107 |
| Boron | Ba | 5 |
| Bromine | Br | 35 |
| Cadmium | Cd | 48 |
| Calcium | Ca | 20 |
| Californium | Cf | 98 |
| Carbon | Ca | 6 |
| Cerium | Ce | 58 |
| Cesium | Cs | 55 |
| Chlorine | Cl | 17 |
| Chromium | Cr | 24 |
| Cobalt | Co | 27 |
| Copernicum | Cn | 112 |
| Copper | Cu | 29 |
| Curium | Cm | 96 |
| Darmstadtium | Ds | 110 |
| Dubnium | Db | 105 |
| Dysprosium | Dy | 66 |
| Einsteinium | Es | 99 |
| Erbium | Er | 68 |
| Europium | Eu | 63 |
| Fermium | Fm | 100 |
| Flerovium | Fl | 114 |
| Fluorine | F | 9 |
| Francium | Fr | 87 |
| Gadolinium | Gd | 64 |
| Gallium | Ga | 31 |
| Germanium | Ge | 32 |
| Gold | Au | 79 |
| Hafnium | Hf | 72 |
| Hassium | Hs | 108 |
| Helium | He | 2 |
| Holmium | Ho | 67 |
| Hydrogen | H | 1 |
| Indium | In | 49 |
| Iodine | In | 53 |
| Iridium | Ir | 77 |
| Iron | Fe | 26 |
| Krypton | Kr | 36 |
| Lanthanum | La | 57 |
| Lawrencium | Lr | 103 |
| Lead | Pb | 82 |
| Lithium | Li | 3 |
| Livermorium | Lv | 116 |
| Lutetium | Lu | 71 |
| Magnesium | Mg | 12 |
| Manganese | Mn | 25 |
| Meitnerium | Mt | 109 |
| Mendelevium | Md | 101 |
| Mercury | Hg | 80 |
| Molybdenum | Mo | 42 |
| Neodymium | Nd | 60 |
| Neon | Ne | 10 |
| Neptunium | Np | 93 |
| Nickle | Ni | 28 |
| Niobium | Nb | 41 |
| Nitrogen | Nb | 7 |
| Nobelium | No | 102 |
| Osmium | Os | 76 |
| Oxygen | Os | 8 |
| Palladium | Pd | 46 |
| Phosphorus | Pb | 15 |
| Platinum | Pt | 78 |
| Plutonium | Pu | 94 |
| Polonium | Po | 84 |
| Potassium | K | 19 |
| Praseodymium | Pr | 59 |
| Promethium | Pm | 61 |
| Protactinium | Pa | 91 |
| Radium | Ra | 88 |
| Radon | Rn | 86 |
| Rhenium | Re | 75 |
| Rhodium | Rh | 45 |
| Roentgenium | Rg | 111 |
| Rubidium | Rb | 37 |
| Ruthenium | Ru | 44 |
| Rutherfordium | Rf | 104 |
| Samarium | Sm | 62 |
| Scandium | Sc | 21 |
| Seaborgium | Sg | 106 |
| Selenium | Se | 34 |
| Silicon | Si | 14 |
| Silver | Ag | 47 |
| Sodium | Na | 11 |
| Strontium | Sr | 38 |
| Sulfur | S | 16 |
| Tantalum | Ta | 73 |
| Technetium | Tc | 43 |
| Tellurium | Te | 52 |
| Terbium | Tb | 65 |
| Thallium | Tl | 81 |
| Thorium | Th | 90 |
| Thulium | Tm | 69 |
| Tin | Si | 50 |
| Titanium | Ti | 22 |
| Tungsten | W | 74 |
| Ununoctium | Uuo | 118 |
| Ununpentium | Uup | 115 |
| Ununseptium | Uus | 117 |
| Ununtrium | Uut | 113 |
| Uranium | U | 92 |
| Vanadium | V | 23 |
| Xenon | Xe | 54 |
| Ytterbium | Yb | 70 |
| Yttrium | Y | 39 |
| Zinc | Zn | 30 |
| Zirconium | Zr | 40 |